Two extremely important principles in electric circuits were codified by Gustav Robert Kirchhoff in the year 1847, known as Kirchhoff’s Laws. His two laws refer to voltages and currents in electric circuits, respectively.
Kirchhoff’s Voltage Law states that the algebraic sum of all voltages in a closed loop is equal to zero. Another way to state this law is to say that for every rise in potential there must be an equal fall, if we begin at any point in a circuit and travel in a loop back to that same starting point.
An analogy for visualizing Kirchhoff’s Voltage Law is hiking up a mountain. Suppose we start at the base of a mountain and hike to an altitude of 5000 feet to set up camp for an overnight stay. Then, the next day we set off from camp and hike farther up another 3500 feet. Deciding we’ve climbed high enough for two days, we set up camp again and stay the night. The next day we hike down 6200 feet to a third location and camp once gain. On the fourth day we hike back to our original starting point at the base of the mountain. We can summarize our hiking adventure as a series of rises and falls like this:
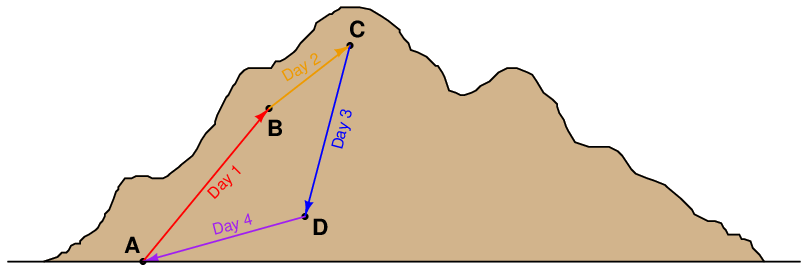
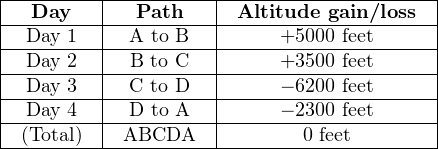
Of course, no one would tell their friends they spent four days hiking a total altitude of 0 feet, so people generally speak in terms of the highest point reached: in this case 8500 feet. However, if we track each day’s gain or loss in algebraic terms (maintaining the mathematical sign, either positive or negative), we see that the end sum is zero (and indeed must always be zero) if we finish at our starting point.
If we view this scenario from the perspective of potential energy as we lift a constant mass from point to point, we would conclude that we were doing work on that mass (i.e. investing energy in it by lifting it higher) on days 1 and 2, but letting the mass do work on us (i.e. releasing energy by lowering it) on days 3 and 4. After the four-day hike, the net potential energy imparted to the mass is zero, because it ends up at the exact same altitude it started at.
Let’s apply this principle to a real circuit, where total current and all voltage drops have already been calculated for us:
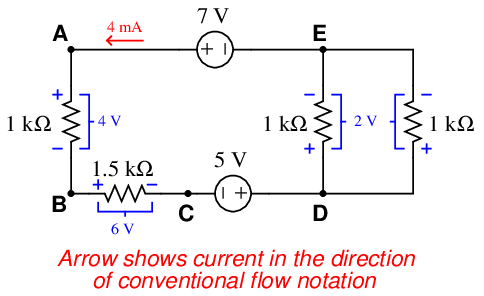
If we trace a path ABCDEA, we see that the algebraic voltage sum in this loop is zero:
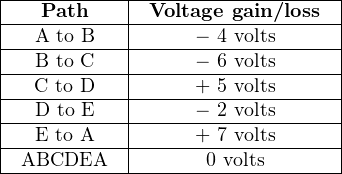
We can even trace a path that does not follow the circuit conductors or include all components, such as EDCBE, and we will see that the algebraic sum of all voltages is still zero:

Kirchhoff’s Voltage Law is often a difficult subject for students, precisely because voltage itself is a difficult concept to grasp. Remember that there is no such thing as voltage at a single point; rather, voltage exists only as a differential quantity. To intelligently speak of voltage, we must refer to either a loss or gain of potential between two points.
Our analogy of altitude on a mountain is particularly apt. We cannot intelligently speak of some point on the mountain as having a specific altitude unless we assume a point of reference to measure from. If we say the mountain summit is 9200 feet high, we usually mean 9200 feet higher than sea level, with the level of the sea being our common reference point. However, our hiking adventure where we climbed 8500 feet in two days did not imply that we climbed to an absolute altitude of 8500 feet above sea level. Since I never specified the sea-level altitude at the base of the mountain, it is impossible to calculate our absolute altitude at the end of day 2. All you can tell from the data given is that we climbed 8500 feet above the mountain base, wherever that happens to be with reference to sea level.
So it is with electrical voltage as well: most circuits have a point labeled as ground where all other voltages are referenced. In DC-powered circuits, this ground point is often the negative pole of the DC power source12 . Voltage is fundamentally a quantity relative between two points: a measure of how much potential has increased or decreased moving from one point to another.
Kirchhoff’s Current Law is a much easier concept to grasp. This law states that the algebraic sum of all currents at a junction point (called a node) is equal to zero. Another way to state this law is to say that for every electron entering a node, one must exit somewhere.
An analogy for visualizing Kirchhoff’s Current Law is water flowing into and out of a “tee” fitting:
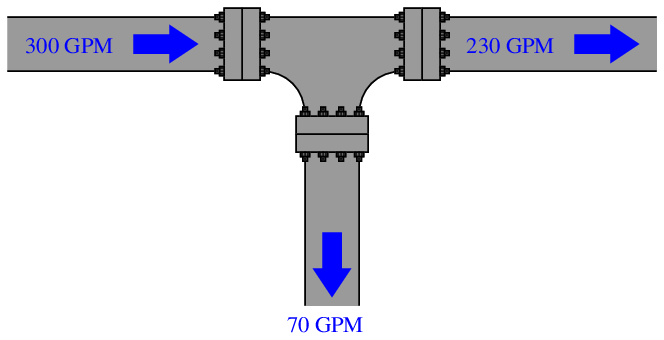
So long as there are no leaks in this piping system, every drop of water entering the tee must be balanced by a drop exiting the tee. For there to be a continuous mis-match between flow rates would imply a violation of the Law of Mass Conservation.
Let’s apply this principle to a real circuit, where all currents have been calculated for us:
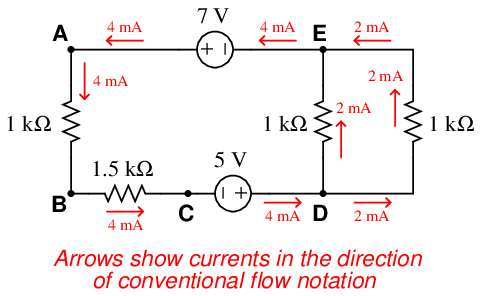
At nodes where just two wires connect (such as points A, B, and C), the amount of current going in to the node exactly equals the amount of current going out (4 mA, in each case). At nodes where three wires join (such as points D and E), we see one large current and two smaller currents (one 4 mA current versus two 2 mA currents), with the directions such that the sum of the two smaller currents form the larger current.
Just as the balance of water flow rates into and out of a piping “tee” is a consequence of the Law of Mass Conservation, the balance of electric currents flowing into and out of a circuit junction is a consequence of the Law of Charge Conservation, another fundamental conservation law in physics.
