Any two electrical conductors separated by an insulating medium possess the characteristic called capacitance: the ability to store energy in the form of an electric field created by a voltage between those two conductors. Capacitance is symbolized by the capital letter C and is measured in the unit of the Farad (F). The relationship between capacitance, stored electric charge (Q), and voltage (V ) is as follows:
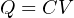
For example, a capacitance having a value of 33 microfarads charged to a voltage of 5 volts would store an electric charge of 165 microcoulombs.
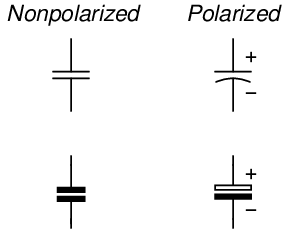
Capacitors are devices expressly designed and manufactured to possess capacitance. They are constructed of a “sandwich” of conductive plates separated by an insulating dielectric. Capacitors have maximum voltage ratings as well as capacitance ratings. Here are some schematic symbols for capacitors:
Although any two conductors separated from each other by an insulating medium possess capacitance, we may optimize the amount of capacitance by situating the conductors in a manner yielding more electric flux for any given amount of applied voltage. Placing the two conductors closer together (thus creating a more intense electric field between them, measured in volts per inch) is one way to increase capacitance. Increasing the overlapping area of the conductors (thus providing more area for parallel electric flux lines to form) is another way. Inserting a strongly dielectric (i.e. an exceptionally good insulating) material between the conductors is a third way to increase capacitance.
These three factors may be expressed in a single mathematical formula for capacitance:
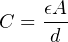
Where,
C = Capacitance in Farads
A = Overlapping area of conductors in square meters
ϵ = Permittivity of the dielectric substance
d = Distance separating the conductors in meters
Capacitance is a non-dissipative quantity. Unlike resistance, a pure capacitance does not dissipate energy in the form of heat; rather, it stores and releases energy from and to the rest of the circuit. We may illustrate the energy-storing behavior of a capacitor by this simple voltage source, switch, and resistor circuit:

Note how the capacitor alternately functions as a source and as a load, depending on what it’s connected to. When connected to a source of voltage, the capacitor absorbs (stores) energy in the form of an electric field between its plates. Current flows through the voltage source in the same direction as though it were powering a load (e.g. a resistor). When the capacitor’s voltage equals the source voltage, current stops in the circuit. Flipping the switch to the “discharge” position connects the capacitor to a resistor, where it discharges its store of energy, acting as a source to the resistor’s load.
Note also how the capacitor maintains the same polarity of voltage during all three steps. Since energy is stored within an electric field inside the capacitor, and electric fields are a function of voltage, the stored energy manifests itself as a voltage with an unchanging polarity. The Law of Energy Conservation – which states energy cannot spontaneously vanish or appear but must be accounted for – tells us a capacitor’s voltage cannot spontaneously vanish, appear, or change polarity. In other words, voltage is the conserved quantity in a capacitor as it transitions between acting as a source and acting as a load. Current through a capacitor, however, switches direction depending on whether the capacitor is charging (acting as a load) or discharging (acting as a source).
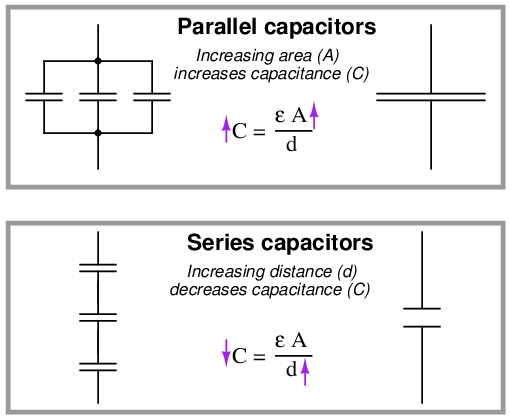
Capacitance adds when capacitors are connected in parallel. It diminishes when capacitors are connected in series:

Recall that capacitance stores energy in the form of an electric field, as a function of the voltage applied to it. It we wish to increase capacitance by connecting multiple capacitors to each other, we need to do that in such a way that each capacitor receives the same (total) applied voltage so that each additional amount of capacitance included in the network will contribute a proportional amount of energy storage to the network. We know voltage is guaranteed to be equal only among parallel-connected components. If we were to connect multiple capacitors in series with one another, their individual voltages would be some fraction of the total voltage (series voltages always adding to equal the total voltage), thus diminishing the energy stored in each capacitor and similarly diminishing the total capacitance.
Another way to comprehend why capacitance increases in parallel and diminishes in series is to consider a network of capacitors as one equivalent capacitor in terms of aggregate plate area and separation distance. Examining the directions of change to the corresponding variables in the permittivity/area/distance formula for capacitance, we see how parallel-connected capacitances must add while series-connected capacitances must diminish:
The relationship between voltage and current for a capacitor is as follows:
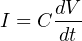
As such, capacitors oppose changes in voltage over time by passing a current. This behavior makes capacitors useful for stabilizing voltage in DC circuits. One way to think of a capacitor in a DC circuit is as a temporary voltage source, always “wanting” to maintain voltage across its terminals as a function of the energy stored within its electric field.
The amount of potential energy (Ep, in units of joules) stored by a capacitor may be determined by altering the voltage/current/capacitance equation to express power (P = IV ) and then applying some calculus (recall that power is defined as the time-derivative of work or energy, P = dW dt = dE dt ):
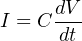
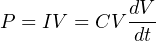
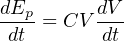
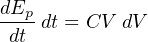
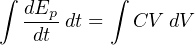
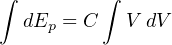
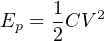
In an AC circuit, the amount of capacitive reactance (XC) offered by a capacitor is inversely proportional to both capacitance and frequency:
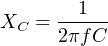
This means an AC signal finds it “easier” to pass through a capacitor (i.e. less ohms of reactance) at higher frequencies than at lower frequencies.