The transformer is one of the most important components in all of AC circuitry. Principally used to “step” between different values of AC voltage and current in power systems, transformers find uses in many other types of circuits including electronic amplifiers (for impedance matching) and even sensor circuits (sensing physical position).
5.4.1 Basic principles
Before exploring the operation of a transformer, it is useful to review the operation of a simple inductor, which is nothing more than a coil of wire usually wrapped around a ferromagnetic core material:
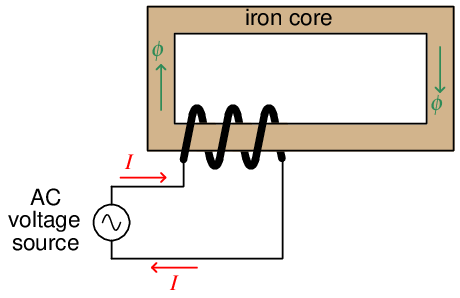
If we apply an alternating (AC) voltage to this coil, it will generate an alternating magnetic field in the core. Just how much magnetic flux (ϕ) will develop in the core depends on how much voltage we apply to the coil. The fundamental relationship between voltage and magnetic flux for any conductive coil is given by Faraday’s Law of Electromagnetic Induction3 :
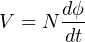
Where,
V = Voltage applied to the coil or induced by the coil (volts)
N = Number of turns of wire
dϕ/dt = Rate of change of magnetic flux (Webers per second)
If the applied voltage is sinusoidal (i.e. shaped like a sine wave), then the magnetic flux magnitude will trace a cosine wave over time. We may demonstrate this mathematically by substituting sinωt (the sine of some frequency ω at any particular point in time t) for V in Faraday’s equation and integrating:

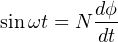
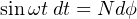
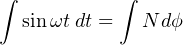
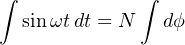
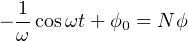
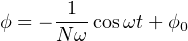
Thus, the amount of magnetic flux (ϕ) in the core at any point in time t is proportional to the cosine of the frequency-time function ωt plus any residual magnetism (ϕ0) the core happened to start out with before any voltage was applied to the coil.
The amount of current drawn by this inductor depends on the reluctance of the core’s magnetic “circuit” and the number of turns in the coil (N). The less reluctance offered by the magnetic path, the less current will be necessary to generate the requisite magnetic field to balance the applied voltage. If we were to take two perfect inductors (i.e. lacking wire resistance) – one with a heavy ferrous core and one with a light ferrous core (or even an air core) – and apply the same AC voltage to them, they would both generate the exact same strength of alternating magnetic field, but the inductor with the lesser core would draw more current from the source in doing so. In other words, the latter inductor would exhibit less reactance (i.e. fewer ohms) to oppose current.
Things get interesting if we wrap a second coil of wire around the same core as the first. For the sake of analysis we will label voltage polarities at one of the peaks of the AC source:
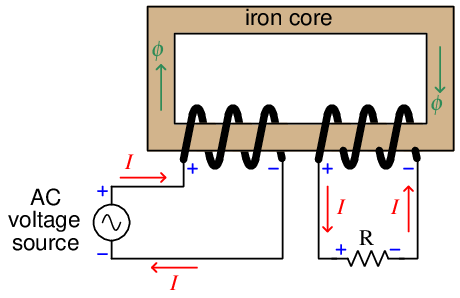
At that moment in time when the top terminal of the source is positive and the bottom terminal is negative, we see that the first coil drops the same voltage (due to self-induction), and that the second coil drops the same voltage as well (due to mutual induction). The polarity of both coils’ voltages are identical because they are wrapped in the same direction around the core and they both experience the same magnetic flux (ϕ). When we examine the directions of current through each coil, however, we see they are opposite one another: the left-hand coil acts as a load (drawing energy from the AC voltage source) while the right-hand coil acts as a source (providing energy to the resistive load).
What we have created here is a true transformer: an electromagnetic component transferring energy from electric form to magnetic form and back again to electric form. The AC voltage source is able to energize the resistive load without direct conductive connection between the two, since the magnetic flux serves as the energy “link” between the two circuits.
Transformers are typically drawn as a set of coils sharing a common core. The coil connected to an electrical source is called the primary, while the coil connected to an electrical load is called the secondary. If the core is ferromagnetic, it is shown as a set of parallel lines between the coils:
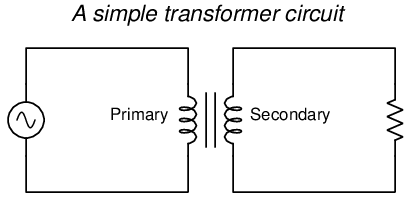
5.4.2 Loading effects
We may explore transformer behavior by observing the effects of powering one with a constant4 -voltage AC source and varying the load resistance:
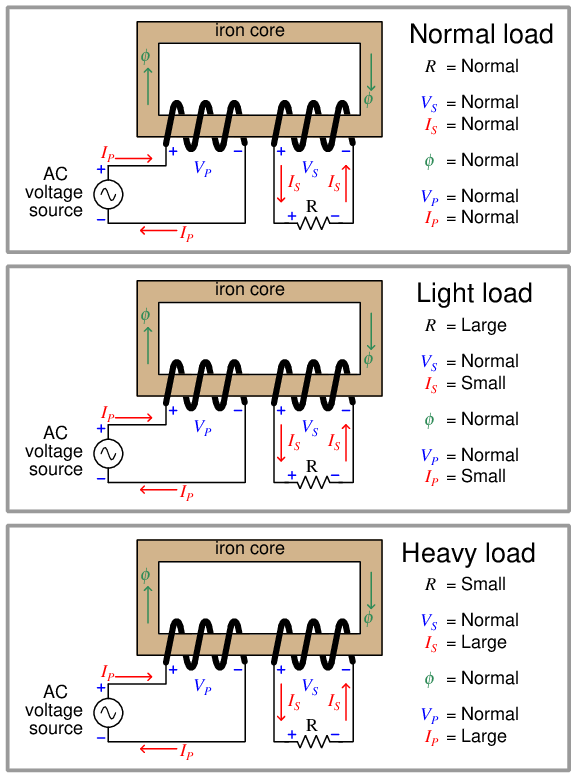
Observe how voltage at both coils is unaffected by load, and similarly how the magnetic flux remains unchanged under different load conditions. The secondary coil acts like a voltage source to the resistive load, reflecting the nature of the primary coil’s source behavior. The magnetic flux amplitude is unaffected by secondary loading in order to satisfy Kirchhoff’s Voltage Law and Faraday’s Law at the primary coil: the coil’s voltage drop must be equal and opposite to the source’s applied voltage, and so the magnetic flux must alternate at the same rates and reach the same peaks so long as the primary source voltage does the same.
Continuing our exploration of transformer behavior, we will now power one with a constant5 -current AC source and vary the load resistance:
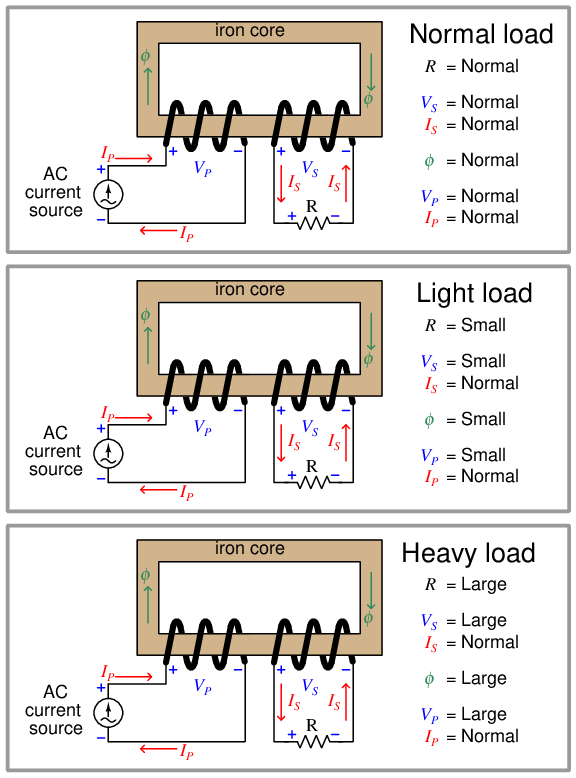
Observe how current now is the unaffected quantity, while voltage and magnetic flux are load-dependent. The secondary coil now acts like a current source to the resistive load, reflecting the nature of the primary coil’s source behavior. As load resistance varies, the secondary coil’s voltage varies proportionately, which in turn demands a commensurate change in magnetic flux.
5.4.3 Step ratios
Transformers are principally used to step between different levels of voltage and current. This is achieved by building the transformer with primary and secondary coils having different numbers of turns. Since both coils share the same magnetic flux, the number of turns will be proportionate to how much voltage is developed at each coil. We may prove this mathematically with Faraday’s Law, using dϕ dt as the quantity shared between primary and secondary coils:


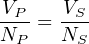
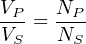
That is to say, the ratio of primary to secondary voltage is the same as the ratio of primary to secondary turns. We may exploit this principle to build transformers delivering the same amount of power to two different load resistances from the same power source, the only difference being the number of turns in the secondary coil:
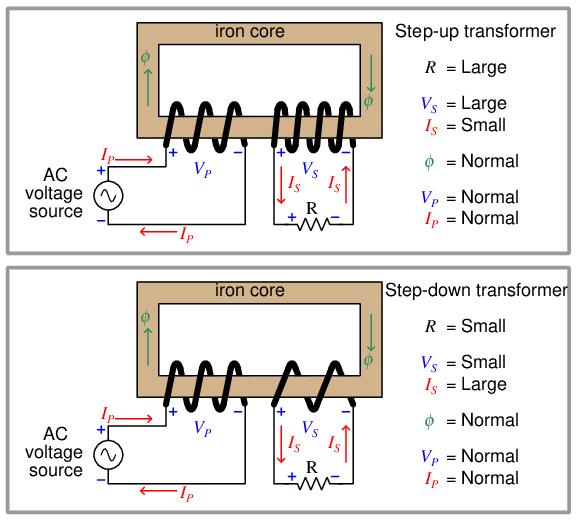
Whichever way a transformer steps voltage from primary to secondary, it must step current the other way.
Here are some quantitative examples, assuming lossless transformers:
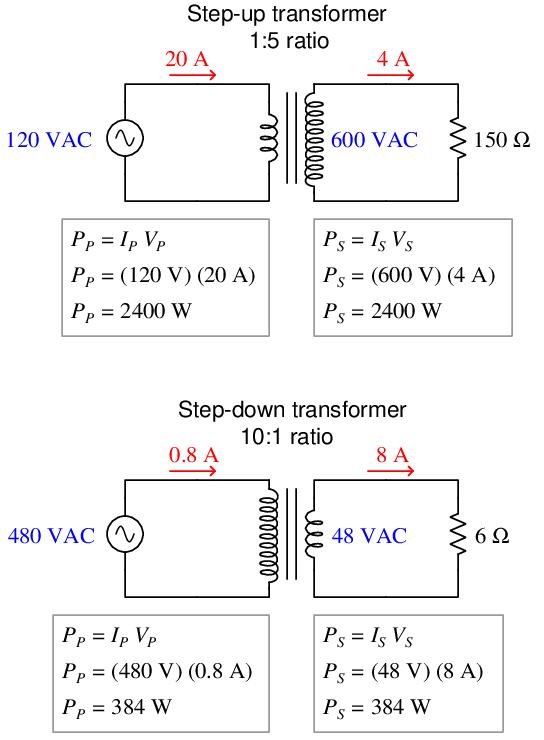
Note how primary and secondary powers are always equal to each other for any given transformer arrangement. Real transformers suffer some internal6 power loss, and as such will exhibit secondary power levels slightly less than primary, but assuming equality provides an easy way to check our voltage and current ratio calculations.
5.4.4 Transformer impedance
An ideal transformer is completely lossless, conveying electrical power from a connected source (on the primary side) to a connected load (on the secondary side) with 100 percent efficiency. Ideal transformers also pose no limit on the amount of power they may couple from primary to secondary winding – in other words, an ideal transformer imposes no inherent limit to power throughput.
Real transformers, however, are not lossless and in fact do act as current-limiting devices. The mechanisms for this include magnetic hysteresis losses, wire resistance, leakage inductance7 , etc.
Consider a thought experiment where we short-circuit the secondary winding of an ideal transformer, which is being powered by an AC voltage source of infinite power capacity (i.e. the source has zero impedance). How much current would pass through the shorted secondary circuit?

This question has no realistic answer. If the 480 VAC source has no current limitation (i.e. is capable of supplying infinite current to a shorted load) and the transformer likewise presents no limit at all to current, the shorted secondary circuit would also experience infinite current, at least in principle.
It should be rather obvious that this scenario cannot exist in the real world. Even with a source of infinite current capability, any realistic transformer would act to impede current delivered to a short-circuit on the secondary side. The question of “how much current would pass through the short-circuit” is really a question of how much impedance the transformer offers.
Let us consider a different thought experiment, this time using a real transformer with a short-circuited secondary winding, powered by a variable AC voltage source:
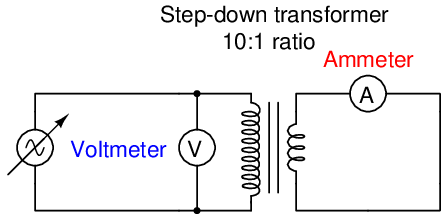
Imagine gradually increasing the source voltage until the secondary circuit ammeter registers a current equal to the transformer’s full-load rating. For an ideal transformer (perfect power coupling), this would happen at some very small amount of voltage applied to the primary winding. Due to the imperfections and losses of real transformers, though, full secondary current will be obtained at a primary voltage equal to some small percentage of the normal (rated) primary voltage. Suppose, for example, our hypothetical transformer with a primary winding rating of 480 VAC outputs full secondary current through a short-circuit at an applied source voltage of only 22 volts. 22 volts is 4.58% of 480 volts, and so we would say this transformer has a measured impedance of 4.58 percent8 .
Although a short-circuited secondary winding scenario may seem contrived, it actually is quite relevant to real-world conditions. In electrical power systems we are often concerned with the maximum amount of current which will flow during fault conditions. If two power conductors directly touch each other, or if a low-resistance arc develops between them through the air, the effect is very nearly a perfect short-circuit. This means transformer impedance will be the dominant factor in limiting fault current: the more impedance a transformer has, the less fault current will manifest during shorted conditions.
One way to apply the impedance percentage value for a power transformer to a fault scenario is to use it as a multiplying factor for secondary current. For example, if a power transformer has a maximum rated secondary current of 180 amps and an impedance rating of 3.3%, the available secondary current into a bolted9 fault will be:
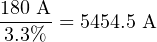
Bolted-fault current calculations are very useful when predicting the amount of energy released in an arc blast incident, which is what happens when an electric arc develops between two closely-spaced conductors in a high-power electric power system. The arc behaves as an extremely low-resistance connection between the conductors, resulting in very large current values with correspondingly high arc temperatures.
Transformer impedance is also useful for calculating the degree to which the output voltage of a power transformer will “sag” below its ideal value when powering a load. Suppose we had a power transformer with a 5:1 turns ratio, designed to receive 120 VAC at its primary winding and output 24 VAC. Under no-load conditions the transformer’s internal impedance will be of no effect, and the transformer will output 24 VAC exactly. However, when a load is connected to the secondary terminals and current begins to flow to power this load, the transformer’s internal impedance will result in the secondary voltage decreasing by a small amount. For example, if this transformer happens to have an impedance of 5.5%, it means the secondary (output) voltage will sag 5.5% below 24 VAC at full load, assuming the primary voltage is maintained at the standard 120 VAC level. 5.5% of 24 volts is 1.32 volts, and so this transformer’s secondary voltage will “sag” from 24 volts down to 22.68 volts (i.e. 1.32 volts less than 24 volts) as load current increases from zero to its full rated value.