22.11 Process/instrument suitability

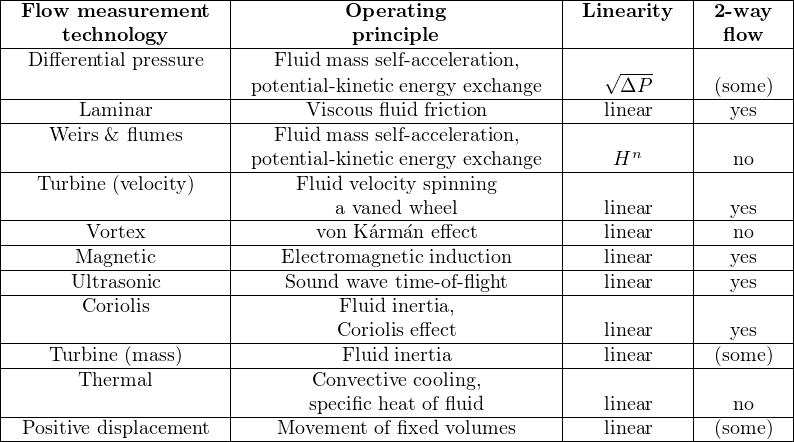
Every flow-measuring instrument exploits a physical principle to measure the flow rate of fluid stream. Understanding each of these principles as they apply to different flow-measurement technologies is the first and most important step in properly applying a suitable technology to the measurement of a particular process stream flow rate. The following table lists the specific operating principles exploited by different flow measurement technologies:

A potentially important factor in choosing an appropriate flowmeter technology is energy loss caused by pressure drop. Some flowmeter designs, such as the common orifice plate, are inexpensive to install but carry a high price in terms of the energy lost in permanent pressure drop (the total, non-recoverable loss in pressure from the inlet of the device to the outlet, not the temporary pressure difference between inlet and vena contracta). Energy costs money, and so industrial facilities would be wise to consider the long-term cost of a flowmeter before settling on the one that is cheapest to install. It could very well be, for example, that an expensive venturi tube will cost less after years of operation than a cheap orifice plate⁸⁰ .

In this regard, certain flowmeters stand above the rest: those with obstructionless flowtubes. Magnetic and ultrasonic flowmeters have no obstructions whatsoever in the path of the flow. This translates to (nearly) zero permanent pressure loss along the length of the tube, and therefore. Thermal mass and straight-tube Coriolis flowmeters are nearly obstructionless, while vortex and turbine meters are only slightly worse.

22.12 Review of fundamental principles

Shown here is a partial listing of principles applied in the subject matter of this chapter, given for the purpose of expanding the reader’s view of this chapter’s concepts and of their general inter-relationships with concepts elsewhere in the book. Your abilities as a problem-solver and as a life-long learner will be greatly enhanced by mastering the applications of these principles to a wide variety of topics, the more varied the better.

• Basic geometrical quantities: distance and velocity are both one-dimensional measurements. Area is a two-dimensional measurement. Volume is a three-dimensional measurement. Relevant to unit conversions for flow measurements. For example, fluid velocity in ft/s, fluid pressure in pounds per ft², volumetric flow in ft³/s.
• Density: the ratio of mass to volume for a particular substance. Relevant to the kinetic energy of a moving fluid, as well as true-mass flow measurement.
• Viscosity: the resistance of a fluid to shear, which may be thought of as the “internal friction” of that fluid. Relevant to whether a fluid moves in laminar or turbulent fashion.
• Laminar flow: a condition where a fluid’s molecules move in parallel paths, never crossing. Relevant to flowmeter selection, because many flowmeters require the flow regime to be turbulent rather than laminar (e.g. orifice plates, thermal mass). Also relevant to certain industrial processes such as mixing and heat transfer, because laminar flow impedes both these processes.
• Turbulent flow: a condition where a fluid’s molecules move chaotically, randomly crossing pathways. Relevant to flowmeter selection, because many flowmeters require the flow regime to be turbulent rather than laminar (e.g. orifice plates, thermal mass). Also required for certain industrial processes such as mixing and heat transfer to efficiently occur.
• Conservation of energy: energy cannot be created or destroyed, only converted between different forms. Relevant to fluid velocities and pressures inside of flow elements such as venturi tubes, orifice plates, Pitot tubes, etc.
• Bernoulli’s equation: z₁ρg+ v₁²ρ 2 +P₁ = z₂ρg+ v₂²ρ 2 +P₂, which is an application of the Law of Energy Conservation, stating that the sum of all forms of energy in a moving fluid stream (height, kinetic, and pressure) must remain the same. Relevant to calculations of pressure drop and pressure recovery across restrictions such as venturi tubes, orifice plates, etc.
• Conservation of mass: mass is an intrinsic property of matter, and as such cannot be created or destroyed. Relevant to the Continuity Principle for moving fluids, where the mass flow rate of a fluid entering a pipe must equal the mass flow rate exiting the pipe, assuming no accumulation or depletion (storage) of mass occurs within the pipe.
• Reynolds number: a unitless value representing the ratio of kinetic to viscous forces in a fluid. The greater the Reynolds number, the more turbulent the flow. The smaller the Reynolds number, the more likely the fluid will move in a laminar fashion. Relevant to many types of flowmeters, which operate accurately only within certain ranges of Reynolds number.
• Flow profile or velocity profile: the relative velocities of a fluid as it moves through a pipe, the velocity at the center being greater than the velocity at the pipe wall. Laminar flow is characterized by large differences in velocity along the profile, while turbulent flow exhibits a “flatter” profile with more consistent velocity across the pipe diameter. Relevant to insertion-type flowmeters such as Pitot tubes where the flowing velocity is sampled at only one point in the flowstream.
• Ideal Gas Law: PV = nRT, describing the relationship between gas pressure, chamber volume, gas quantity (in moles), and gas temperature. Relevant to measurements of gas flow rate at different pressures and temperatures (e.g. converting between “actual” or “flowing” units and “standard” units of gas measurement).
• Newton’s Second Law of motion: F = ma, describing how the acceleration of an object is directly proportional to the amount of applied (resultant) force and inversely proportional to its mass. Relevant to the development of a pressure difference across a flow element where the fluid molecules must either accelerate (positive a) or decelerate (negative a).
• Inverse mathematical functions: an inverse function, when applied to the result of its counterpart function, “un-does” the operation and leaves you with the original quantity. Relevant to the application of “square-root” in DP-based flow measurements. The natural characteristic of an accelerating or decelerating flow element (e.g. orifice plate) is to generate a pressure drop proportional to the square of the flow rate. Therefore, we must “square-root” that pressure signal in order to infer flow rate.
• Wavelength vs. frequency: v = λf, describing the relationship between wavelength (λ) and frequency (f) for a wave. Relevant to vortex-shedding flowmeters, where the frequency is directly proportional to the velocity of the fluid. Also relevant to ultrasonic flowmeters.
• Time, velocity, and distance: x = vt, describing the relationship between velocity (v), time of travel (t), and distance traveled (x). Relevant to ultrasonic flowmeters, where travel time of an ultrasonic sound wave is used to calculate fluid velocity.
• Speed of sound through a substance: varies directly with the bulk modulus of the substance and inversely with the mass density of the substance as described by the formula c = . Relevant to Doppler-style ultrasonic flowmeters, where the Doppler frequency shift depends on the speed of sound through the fluid.
• Resonance: when something oscillates at its natural frequency. Relevant to Coriolis flowmeters, whose tubes are made to vibrate at their resonant frequency in order to measure fluid density. For a vibrating string (which closely approximates a vibrating tube), resonant frequency is directly proportional to string tension and inversely proportional to both length and mass as described by the formula f = 1 _ 2L.
• Specific heat: the amount of heat necessary to change the temperature of a some substance per unit mass and per unit of temperature. Relevant to thermal flowmeters, which work on the principle of heat transfer from a heated object to the moving fluid. The greater the mass flow rate of the fluid, the greater the heat transfer rate for any given specific heat value of the fluid. Specific heat is a function of the fluid’s chemical composition.
• Scintillation: the random and time-varying warping of light rays due to pockets of fluid having different refractive indices. Variations in temperature will cause this, as will turbulent motion of the fluid. Relevant to certain types of optical flowmeter, which pass light through a flowstream and look for patterns of scintillation after the light has traveled through the moving fluid.
• Differentiation (calculus): where one variable is proportional to the rate-of-change of two others. Differentiation always results in a division (quotient) of units. Relevant to calculations of flow rate based on mass or volume. Volumetric flow rate (Q) is equal to the rate of change in fluid volume over time (Q = dV _ dt ). Mass flow rate (W) is equal to the rate of change in fluid mass over time (W = dm dt )
• Integration (calculus): where one variable is proportional to the accumulation of the product of two others. Integration always results in a multiplication of units. Relevant to calculations of mass or volume based on flow rate. Total volume of fluid passed by a point in a pipe (V ) equal to the integral of volumetric flow rate times time: V = ∫ Qdt. Total mass of fluid passed by a point in a pipe (m) equal to the integral of mass flow rate times time: m = ∫ W dt.

References

AGA Report No. 3 – Orifice metering of natural gas and other related hydrocarbon fluids, Part 1 (General Equations and Uncertainty Guidelines), Catalog number XQ9017, American Gas Association and American Petroleum Institute, Washington D.C., Third Edition October 1990, Second Printing June 2003.

AGA Report No. 3 – Orifice metering of natural gas and other related hydrocarbon fluids, Part 2 (Specification and Installation Requirements), Catalog number XQ0002, American Gas Association and American Petroleum Institute, Washington D.C., Fourth Edition April 2000, Second Printing June 2003.

AGA Report No. 3 – Orifice metering of natural gas and other related hydrocarbon fluids, Part 3 (Natural Gas Applications), Catalog number XQ9210, American Gas Association and American Petroleum Institute, Washington D.C., Third Edition August 1992, Second Printing June 2003.

AGA Report No. 3 – Orifice metering of natural gas and other related hydrocarbon fluids, Part 4 (Background, Development, Implementation Procedure, and Subroutine Documentation for Empirical Flange-Tapped Discharge Coefficient Equation), Catalog number XQ9211, American Gas Association and American Petroleum Institute, Washington D.C., Third Edition October 1992, Second Printing August 1995, Third Printing June 2003.

Chow, Ven Te., Open-Channel Hydraulics, McGraw-Hill Book Company, Inc., New York, NY, 1959.

“Daniel Gas Ultrasonic Flow Meter Brochure”, document DAN-USM-B-FAMILY-0405, Daniel Measurement and Control, Inc., Emerson Process Management, 2005.

“Daniel Ultrasonic Gas Flowmeter Reference, Installation and Operations Manual”, part number 3-9000-740, revision H, Daniel Measurement and Control, Inc., Emerson Process Management, 2007.

“Flow Measurement User Manual”, Form Number A6043, Part Number D301224X012, Emerson Process Management, 2005.

Freund, William; Zanker, Klaus; Goodson, Dale; Hall, James E.; Jamieson, Andrew W.; “Operation of Ultrasonic Flow Meters at Conditions Different from their Calibration”, Paper 2.2, North Sea Flow Measurement Workshop, October 22-25, 2002.

Fribance, Austin E., Industrial Instrumentation Fundamentals, McGraw-Hill Book Company, New York, NY, 1962.

General Specifications: “EJX910A Multivariable Transmitter”, Document GS 01C25R01-01E, 5th edition, Yokogawa Electric Corporation, Tokyo, Japan, 2005.

Giancoli, Douglas C., Physics for Scientists & Engineers, Third Edition, Prentice Hall, Upper Saddle River, NJ, 2000.

Hanlon, Paul C., Compressor Handbook, The McGraw-Hill Companies, New York, NY, 2001.

Hofmann, Friedrich, Fundamentals of Ultrasonic Flow Measurement for industrial applications, Krohne Messtechnik GmbH & Co. KG, Duisburg, Germany, 2000.

Hofmann, Friedrich, Fundamental Principles of Electromagnetic Flow Measurement, 3rd Edition, Krohne Messtechnik GmbH & Co. KG, Duisburg, Germany, 2003.

“How Today’s Ultrasonic Meter Diagnostics Solve Metering Problems”, Daniel Measurement and Control, Inc., Emerson Process Management, 2010.

Improving Compressed Air System Performance – a sourcebook for industry, U.S. Department of Energy, Washington, DC, 2003.

Kallen, Howard P., Handbook of Instrumentation and Controls, McGraw-Hill Book Company, Inc., New York, NY, 1961.

Keisler, H. Jerome, Elementary Calculus – An Infinitesimal Approach, Second Edition, University of Wisconsin, 2000.

Lipták, Béla G. et al., Instrument Engineers’ Handbook – Process Measurement and Analysis Volume I, Fourth Edition, CRC Press, New York, NY, 2003.

Miller, Richard W., Flow Measurement Engineering Handbook, Second Edition, McGraw-Hill Publishing Company, New York, NY, 1989.

Parker, Jody; Stobie, Gordon; Melnyk, Ivan; Letton, Chip; “Flare Metering With Optics – From Blue-Sky Technology to the Real World”, 25th International North Sea Flow Measurement workshop, Oslo, Norway, October 16-19, 2007.

Parshall, R. L., “Measuring Water in Irrigation Channels”, Farmers’ Bulletin number 1683, pages 1-29, Washington D.C., 1941.

Price, James F., A Coriolis Tutorial, version 3.3, Woods Hole Oceanographic Institution, Woods Hole, MA, 2006.

“Proving Coriolis Flowmeters”, document 1004732, Revision A, Micro Motion, Inc., Boulder, CO, October 1998.

Spink, L. K., Principles and Practice of Flow Meter Engineering, Ninth Edition, The Foxboro Company, Foxboro, MA, 1967.

Tech-Spec: “SCFM (Standard CFM) vs. ACFM (Actual CFM)”, Reference 15-010504.006, Sullair Corporation, 2004.

“Top Mount Installation for DP Flowmeters in Steam Service”, whitepaper number 00870-0200-4809, Emerson Process Management, August 2009.

Vennard, John K., Elementary Fluid Mechanics, 3rd Edition, John Wiley & Sons, Inc., New York, NY, 1954.

Wang, Ting-I; Buhr, Eric; “Optical Flow Sensing: A New Approach to an Old Problem”, May 2001.

Zanker, Klaus J., “Diagnostic Ability of the Daniel Four Path Ultrasonic Flow Meter”, Daniel Measurement and Control, Inc., Emerson Process Management, 2010.

Back to Main Index of Book