An interesting parallel to the “unity fraction” unit conversion technique is something referred to in physics as dimensional analysis. Performing dimensional analysis on a physics formula means to set it up with units of measurement in place of variables, to see how units cancel and combine to form the appropriate unit(s) of measurement for the result.
For example, let’s take the familiar power formula used to calculate power in a simple DC electric circuit:
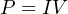
Where,
P = Power (watts)
I = Current (amperes)
V = Voltage (volts)
Each of the units of measurement in the above formula (watt, ampere, volt) are actually comprised of more fundamental physical units. One watt of power is one joule of energy transferred per second. One ampere of current is one coulomb of electric charge moving by per second. One volt of potential is one joule of energy per coulomb of electric charge. When we write the equation showing these units in their proper orientations, we see that the result (power in watts, or joules per second) actually does agree with the units for amperes and volts because the unit of electric charge (coulombs) cancels out. In dimensional analysis we customarily distinguish unit symbols from variables by using non-italicized letters and surrounding each one with square brackets:
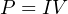
![[Watts] = [Amperes]× [Volts] or [W ] = [A ][V]](https://www.technocrazed.com/books/Instrumentation/Book_half125x.png)
![[ Joules ] [Coulombs] [ Joules ] [J] [C ][ J]
Seconds = -Seconds-- × Coulombs- or s = -s C-](https://www.technocrazed.com/books/Instrumentation/Book_half126x.png)
Dimensional analysis gives us a way to “check our work” when setting up new formulae for physics- and chemistry-type problems.