Voltage is the amount of specific potential energy available between two points in an electric circuit. Potential energy is energy that is potentially available to do work. Looking at this from a classical physics perspective, potential energy is what we accumulate when we lift a weight above ground level, or when we compress a spring:
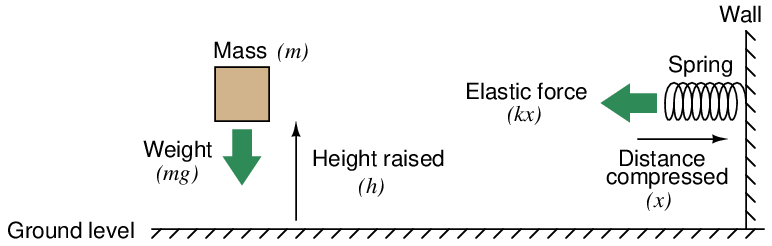
In either case, potential energy is calculated by the work done in exerting a force over a parallel distance. In the case of the weight, potential energy (Ep) is the simple product of weight (gravity g acting on the mass m) and height (h):
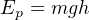
Energy calculations for springs are more complex than for weights. The force exerted by the spring against the compressing motion increases with compression (F = kx, where k is the elastic constant of the spring). It does not remain steady as the force of weight does for the lifted mass. Therefore, the potential energy equation is nonlinear:
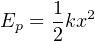
Releasing the potential energy stored in these mechanical systems is as simple as dropping the mass, or letting go of the spring. The potential energy will return to the original condition (zero) when the objects are at rest in their original positions. If either the mass or the spring were attached to a machine to harness the return-motion, that stored potential energy could be used to do useful tasks.
Potential energy may be similarly defined and quantified for any situation where we exert a force over a parallel distance, regardless of where that force or the motivating distance comes from. For instance, the static cling you experience when you pull a wool sock out of a clothes dryer is an example of a force. By pulling that sock away from another article of clothing against the force of “static cling,” you are doing work, and storing potential energy in the tension between that sock and the rest of the clothing. In a similar manner, that stored energy could be released to do useful tasks if we placed the sock in some kind of machine harnessing the sock’s motion as it returns to its original position on the pile of laundry, pulled by the force of static electrical attraction.
If we make use of non-mechanical means to move electric charge from one location to another, the result is no different. Moving attracting charges apart from one another means doing work (a force exerted over a parallel distance) and storing potential energy in that physical tension. When we use chemical reactions to move electrons from one metal plate to another in a solution, or when we spin a generator and electro-magnetically motivate electrons to seek other locations, we impart potential energy to those electrons. We could express this potential energy in the same unit as we do for mechanical systems (the Joule). However, it is actually more useful to express the potential energy in an electric system in terms of how many joules are available per a specific quantity of electric charge (a certain number of electrons). This measure of specific potential energy is simply called electric potential or voltage, and we measure it in units of Volts, in honor of the Italian physicist Alessandro Volta, inventor of the first electrochemical battery.
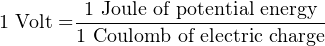
In other words, if we forced 1 Coulomb’s worth of electrons (6.24 × 1018 of them, to be exact) away from a positively-charged place, and did one Joule’s worth of work in the process, we would have generated one Volt of electric potential.
Electric potential (voltage) and potential energy share a common, yet confusing property: both quantities are fundamentally relative between two physical locations. There is really no such thing as specifying a quantity of potential energy at a single location. The amount of potential energy in any system is always relative between two different points. If I lift a mass off the ground, I can specify its potential energy, but only in relation to its former position on the ground. The amount of energy that mass is potentially capable of releasing by free-fall depends on how far it could possibly fall. To illustrate, we will perform some “thought experiments” where we lift a 1 kilogram mass 1 meter off the ground and then drop that mass to assess its energy. That 1-kilo mass weighs 9.81 Newtons on Earth, and the distance lifted was 1 meter, so the potential energy stored in the mass is 9.81 joules, right? Consider the following scenario:
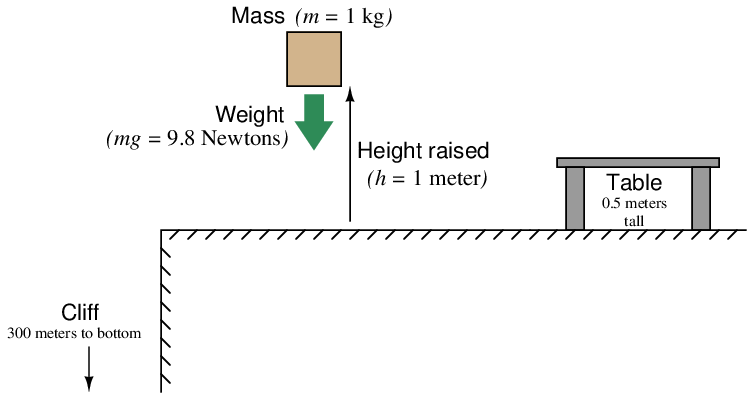
If we drop the mass over the spot we first lifted it from, it will release all the potential energy we invested in it: 9.81 joules. From this example it seems very clear that the mass possessed 9.81 joules of potential energy when lifted. However, the situation becomes more complicated if we carry the mass over to the table and release it there. Since the mass can now only fall half a meter, it will only release 4.9 joules of energy in the process. How much potential energy did the mass have while suspended above that table? If you argue that the mass possessed a full 9.81 joules of potential energy at that original height, then why can’t we realize that full potential when dropped over the table? Can we really say that an object possess potential energy if we cannot realize that potential?
Next, imagine lifting the 1 kg mass 1 meter off the ground, and then carrying it over the edge of a cliff with a 300 meter drop. If we were to release the mass here, it would fall a full 301 meters before hitting the ground. This represents 2.95 kilojoules (kJ) of energy! How can we possibly argue that the mass had a potential energy of 9.81 joules when lifted one meter off the ground, and then without imparting any more energy to that mass we suddenly are able to realize over 300 times as much energy?
The answer to this paradox is that potential energy is always relative between the object’s initial height and its height after falling. It is technically incorrect to say that the mass possesses 9.81 joules of potential energy when lifted 1 meter off the ground, as though potential energy were an absolute quantity. Instead, it is more accurate to say that the mass gained 9.81 joules of potential energy after being lifted 1 meter off the ground, implying that the mass could have possessed potential energy (with reference to the cliff’s bottom) even while sitting on the ground (above the cliff).
Likewise, electrical voltage (as an expression of potential energy) is a quantity relative between two points. Electrical voltage is symbolized by the variable V and measured in the unit of the Volt. Just as we must know the mass’s position relative to its falling point before we can quantify its potential energy, we must know an electric charge’s position relative to its return point before we can quantify its voltage. Consider a series of batteries1 connected as shown:
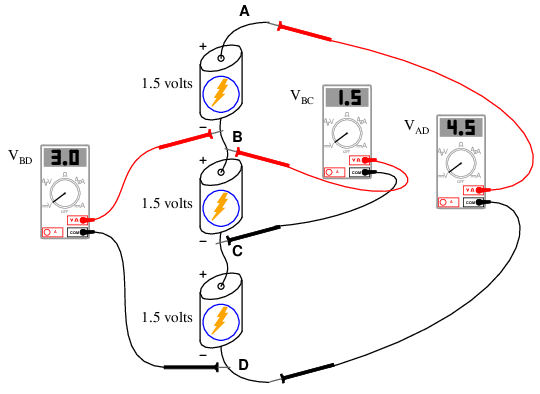
The voltage as measured between any two points directly across a single battery will be 1.5 volts:
V AB = 1.5 volts
V BC = 1.5 volts
V CD = 1.5 volts
If, however, we span more than one battery with our voltmeter connections, our voltmeter will register more than 1.5 volts:
V AC = 3.0 volts
V BD = 3.0 volts
V AD = 4.5 volts
Thus we see there is no such thing as “voltage” at a single point in a circuit. The concept of voltage has meaning only between pairs of points in a circuit, just as the concept of potential energy for a mass has meaning only between two physical locations: where the mass is, and where it may potentially fall.
Things get interesting when we connect voltage sources in different configurations. Consider the following example, identical to the previous illustration except the middle battery has been reversed:
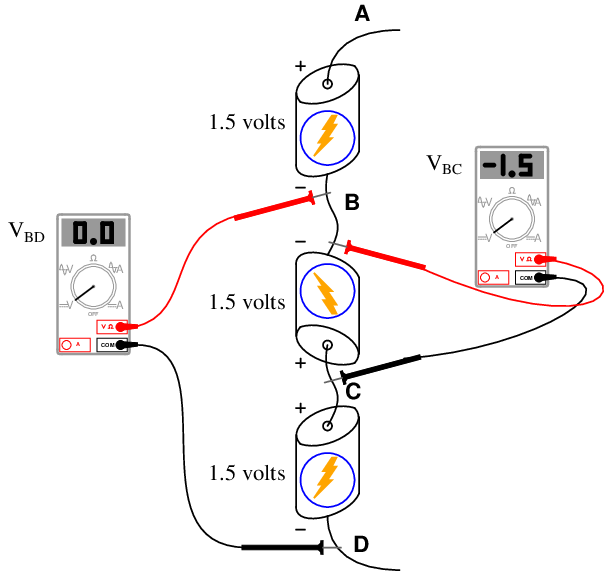
Note the “+” and “−” signs next to the ends of the batteries. These signs show the polarity of each battery’s voltage. Also note how the two voltmeter readings are different from before. Here we see an example of negative potential with the middle battery connected in opposition to the other two batteries. While the top and bottom batteries are both “lifting” electric charges to greater potential (going from point D to point A), the middle battery is decreasing potential from point C to point B. It’s like taking a step forward, then a step back, then another step forward. Or, perhaps more appropriately, like lifting a mass 1.5 meters up, then setting it down 1.5 meters, then lifting it 1.5 meters up again. The first and last steps accumulate potential energy, while the middle step releases potential energy.
This explains why it is important to install multiple batteries the same way into battery-powered devices such as radios and flashlights. The batteries’ voltages are supposed to add to a make a larger total required by the device. If one or more batteries are placed backwards, potential will be lost instead of gained, and the device will not receive enough voltage.
Here we must pay special attention to how we use our voltmeter, since polarity matters. All voltmeters are standardized with two colors for the test leads: red and black. To make sense of the voltmeter’s indication, especially the positive or negative sign of the indication, we must understand what the red and black test lead colors mean:
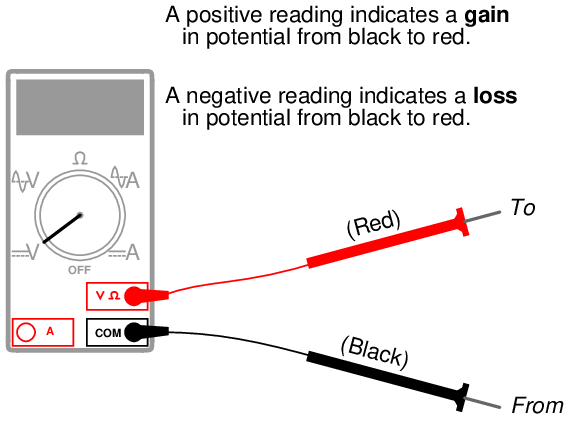
Connecting these test leads to different points in a circuit will tell you whether there is potential gain or potential loss from one point (black) to the other point (red).