Temperature measurement devices may be classified into two broad types: contact and non-contact. Contact-type temperature sensors detect temperature by directly touching the material to be measured, and there are several varieties in this category. Non-contact temperature sensors work by detecting light emitted by hot objects.
Energy radiated in the form of electromagnetic waves (photons, or light) relates to object temperature by an equation known as the Stefan-Boltzmann equation, which tells us the rate of heat lost by radiant emission from a hot object is proportional to the fourth power of its absolute temperature:
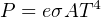
Where,
P = Radiated energy power (watts)
e = Emissivity factor (unitless)
σ = Stefan-Boltzmann constant (5.67 × 10−8 W / m2 ⋅ K4)
A = Surface area (square meters)
T = Absolute temperature (Kelvin)
Solving for temperature (T) involves the use of the fourth root, to “un-do” the fourth power function inherent to the original function:
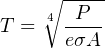
Any optical temperature sensor measuring the emitted power (P) must “characterize” the power measurement using the above equation to arrive at an inferred temperature. This characterization is typically performed inside the temperature sensor by a microcomputer.
26.5 Analytical measurements
A great many chemical composition measurements may be made indirectly by means of electricity, if those measurements are related to the concentration of ions (electrically charged molecules). Such measurements include:
- pH of an aqueous solution
- Oxygen concentration in air
- Ammonia concentration in air
- Lead concentration in water
The basic principle works like this: two different chemical samples are placed in close proximity to each other, separated only by an ion-selective membrane able to pass the ion of interest. As the ion activity attempts to reach equilibrium through the membrane, an electrical voltage is produced across that membrane. If we measure the voltage produced, we can infer the relative activity of the ions on either side of the membrane.
Not surprisingly, the function relating ion activity to the voltage generated is nonlinear. The standard equation describing the relationship between ionic activity on both sides of the membrane and the voltage produced is called the Nernst equation:
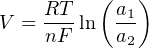
Where,
V = Electrical voltage produced across membrane due to ion exchange (volts)
R = Universal gas constant (8.315 J/mol⋅K)
T = Absolute temperature (Kelvin)
n = Number of electrons transferred per ion exchanged (unitless)
F = Faraday constant (96485 coulombs per mole)
a1 = Activity of ion in measured sample
a2 = Activity of ion in reference sample (on other side of membrane)
A practical application for this technology is in the measurement of oxygen concentration in the flue gas of a large industrial burner, such as what might be used to heat up water to generate steam. The measurement of oxygen concentration in the exhaust of a combustion heater (or boiler) is very important both for maximizing fuel efficiency and for minimizing pollution (specifically, the production of NOx molecules). Ideally, a burner’s exhaust gas will contain no oxygen, having consumed it all in the process of combustion with a perfect stoichiometric mix of fuel and air. In practice, the exhaust gas of an efficiently-controlled burner will be somewhere near 2%, as opposed to the normal 21% of ambient air.
One way to measure the oxygen content of hot exhaust is to use a high-temperature zirconium oxide detector. This detector is made of a “sandwich” of platinum electrodes on either side of a solid zirconium oxide electrolyte. One side of this electrochemical cell is exposed to the exhaust gas (process), while the other side is exposed to heated air which serves as a reference:
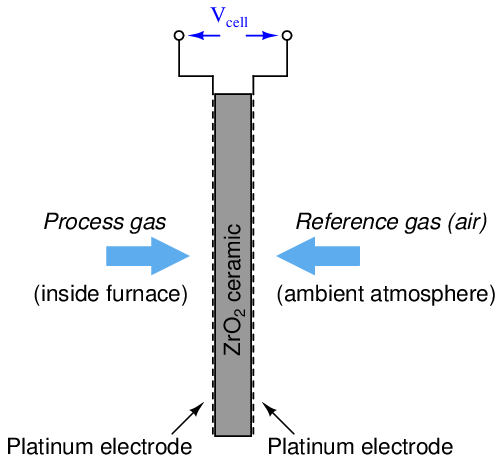
The electrical voltage generated by this “sandwich” of zirconium and platinum is sent to an electronic amplifier circuit, and then to a microcomputer which applies an inverse function to the measured voltage in order to arrive at an inferred measurement for oxygen concentration. This type of chemical analysis is called potentiometric, since it measures (“metric”) based on an electrical voltage (“potential”).
The Nernst equation is an interesting one to unravel, to solve for ion activity in the sample (a1) given voltage (V ):
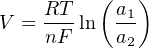
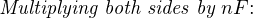
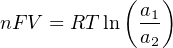
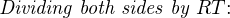
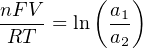
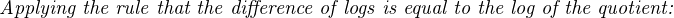
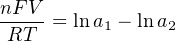
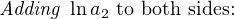
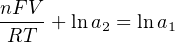
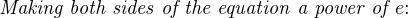
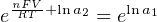
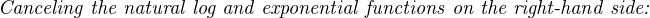
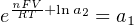
In most cases, the ionic activity of a2 will be relatively constant, and so lna2 will be relatively constant as well. With this in mind, we may simplify the equation further, using k as our constant value:
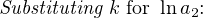
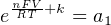
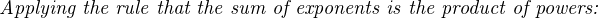
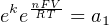
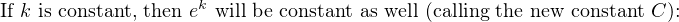
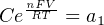
Analytical instruments based on potentiometry must evaluate this inverse function to “undo” the Nernst equation to arrive at an inferred measurement of ion activity in the sample given the small voltage produced by the sensing membrane. These instruments typically have temperature sensors as well built in to the sensing membrane assembly, since it is apparent that temperature (T) also plays a role in the generation of this voltage. Once again, this mathematical function is typically evaluated in a microprocessor.
26.6 Review of fundamental principles
Shown here is a partial listing of principles applied in the subject matter of this chapter, given for the purpose of expanding the reader’s view of this chapter’s concepts and of their general inter-relationships with concepts elsewhere in the book. Your abilities as a problem-solver and as a life-long learner will be greatly enhanced by mastering the applications of these principles to a wide variety of topics, the more varied the better.
- Inverse mathematical functions: an inverse function, when applied to the result of its counterpart function, “un-does” the operation and leaves you with the original quantity. Relevant to all manner of “linearization” techniques designed to make an inherently nonlinear measurement read linearly.
- Bernoulli’s equation: z1ρg+ v12ρ 2 +P1 = z2ρg+ v22ρ 2 +P2, which is an application of the Law of Energy Conservation, stating that the sum of all forms of energy in a moving fluid stream (height, kinetic, and pressure) must remain the same. Relevant to calculations of pressure drop and pressure recovery across restrictions such as venturi tubes, orifice plates, etc.
- Nernst equation: V = RT nF ln predicting the amount of voltage developed across an ion-permeable membrane by the exchange of ions across that membrane. Relevant to all forms of potentiometric chemical analysis, where sensor voltage is proportional to the logarithm of concentration quotient across the sensor membrane.
References
Lipták, Béla G. et al., Instrument Engineers’ Handbook – Process Measurement and Analysis Volume I, Fourth Edition, CRC Press, New York, NY, 2003.
Stewart, James, Calculus: Concepts and Contexts, 2nd Edition, Brooks/Cole, Pacific Grove, CA, 2001.