A fluid is any substance having the ability to flow: to freely change shape and move under the influence of a motivating force. Fluid motion may be analyzed on a microscopic level, treating each fluid molecule as an individual projectile body. This approach is extraordinarily tedious on a practical level, but still useful as a model of fluid behavior.
Some fluid properties are accurately predicted by this model, especially predictions dealing with potential and kinetic energies. However, the ability of a fluid’s molecules to independently move give it unique properties that solids do not possess. One of these properties is the ability to effortlessly transfer pressure, defined as force applied over area.
2.11.1 Pressure
The common phases of matter are solid, liquid, and gas. Liquids and gases are fundamentally distinct from solids in their intrinsic inability to maintain a fixed shape. In other words, liquids and gases tend to fill whatever solid containers they are held in. Similarly, both liquids and gases both have the ability to flow, which is why they are collectively called fluids.
Due to their lack of definite shape, fluids tend to disperse any force applied to them. This stands in marked contrast to solids, which tend to transfer force only in the applied direction. Take for example the force transferred by a nail, from a hammer to a piece of wood:
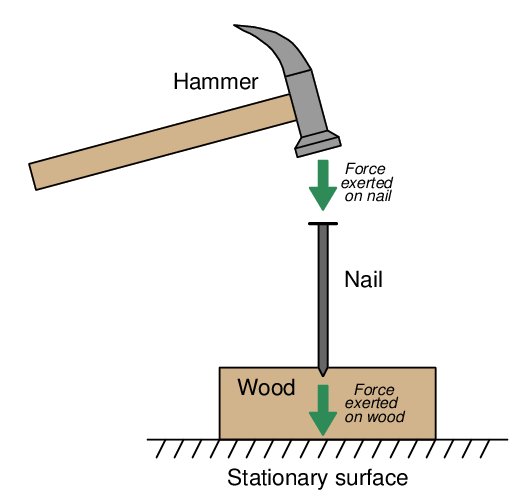
The impact of the hammer’s blow is directed straight through the solid nail into the wood below – nothing surprising here.
Now consider what a fluid would do when subjected to the same hammer blow:
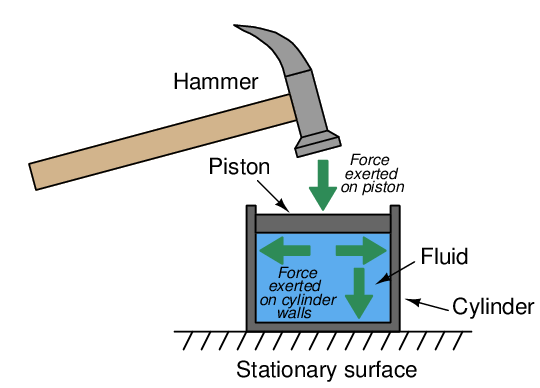
Given the freedom of a fluid’s molecules to move about, the impact of the hammer blow becomes directed everywhere against the inside surface of the container (the cylinder). This is true for all fluids: liquids and gases alike. The only difference between the behavior of a liquid versus a gas in the same scenario is that the gas will compress (i.e. the piston will move down as the hammer struck it), whereas the liquid will not compress (i.e. the piston will remain in its resting position). Gases yield under pressure, liquids do not.
It is very useful to quantify force applied to a fluid in terms of force per unit area, since the force applied to a fluid becomes evenly dispersed in all directions to the surface containing it. This is the definition of pressure60 (P): the amount of force (F) distributed across a given area (A).
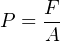
In the metric system, the standard unit of pressure is the pascal (Pa), defined as one Newton (N) of force per square meter (m2) of area. In the British system of measurement, the standard unit of pressure is the PSI: pounds (lb) of force per square inch (in2) of area. Pressure is often expressed in units of kilopascals (kPa) when metric units are used because one pascal is a rather small61 pressure for most engineering applications.
The even distribution of force throughout a fluid has some very practical applications. One application of this principle is the hydraulic lift, which functions somewhat like a fluid lever:
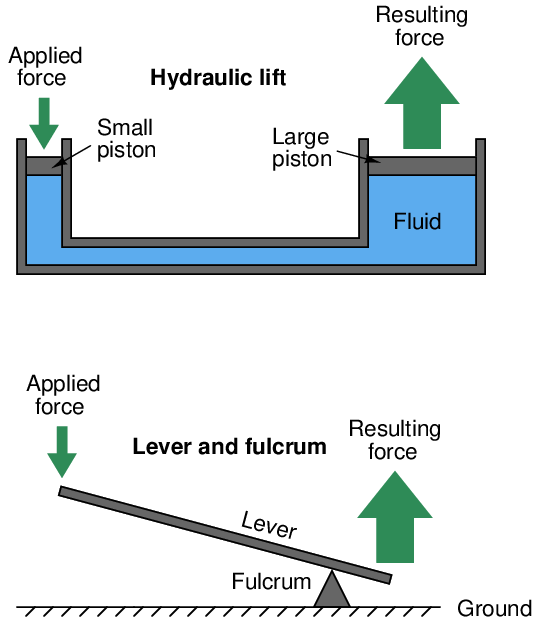
Force applied to the small piston creates a pressure throughout the fluid. That pressure exerts a greater force on the large piston than what is exerted on the small piston, by a factor equal to the ratio of piston areas. Since area for a circular piston is proportional to the square of the radius (A = πr2), even modest ratios of piston diameter yield large ratios of area and therefore of force. If the large piston has five times the area of the small piston (i.e. the large piston’s diameter is 2.236 times greater than the small piston’s diameter), force will be multiplied five-fold. Just as with the lever, however, there must be a trade-off so as to not violate the Conservation of Energy. The trade-off for increased force is decreased distance, whether in the lever system or in the hydraulic lift system. If the large piston generates a force five times greater than what is applied to the small piston, it must move only one-fifth as far as the small piston’s motion. In this way, energy in equals energy out (remember that work, which is equivalent to energy, is calculated by multiplying force by parallel distance traveled).
For those familiar with electricity, what you see here in either the lever system or the hydraulic lift is analogous to a transformer: we can step AC voltage up, but only by reducing AC current. Being a passive device, a transformer cannot boost power. Therefore, power out can never be greater than power in, and given a perfectly efficient transformer, power out will always be precisely equal to power in:
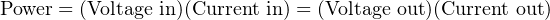
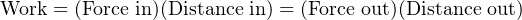
Fluid may be used to transfer power just as electricity is used to transfer power. Such systems are called hydraulic if the fluid is a liquid (usually oil), and pneumatic if the fluid is a gas (usually air). In either case, a machine (pump or compressor) is used to generate a continuous fluid pressure, pipes are used to transfer the pressurized fluid to the point of use, and then the fluid is allowed to exert a force against a piston or a set of pistons to do mechanical work:

An interesting use of fluid we see in the field of instrumentation is as a signaling medium, to transfer information between places rather than to transfer power between places. This is analogous to using electricity to transmit voice signals in telephone systems, or digital data between computers along copper wire. Here, fluid pressure represents some other quantity, and the principle of force being distributed equally throughout the fluid is exploited to transmit that representation to some distant location, through piping or tubing:
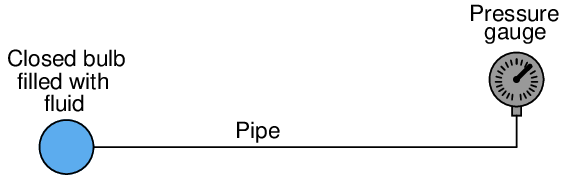
This illustration shows a simple temperature-measuring system called a filled bulb, where an enclosed bulb filled with fluid is exposed to a temperature that we wish to measure. A rise in temperature makes the fluid expand and thereby increases pressure sensed at the gauge. The purpose of the fluid here is two-fold: first to sense temperature, and second to relay this temperature measurement a long distance away to the gauge. The principle of even pressure distribution allows the fluid to act as a signal medium to convey the information (bulb temperature) to a distant location.
2.11.2 Pascal’s Principle and hydrostatic pressure
We learned earlier that fluids tend to evenly distribute any applied force. This fundamental principle is the basis of fluid power and fluid signaling systems, where pressure is assumed to be transferred equally to all points in a confined fluid. In the example of a hydraulic lift given earlier, we assume that the pressure throughout the fluid pathway is equal:
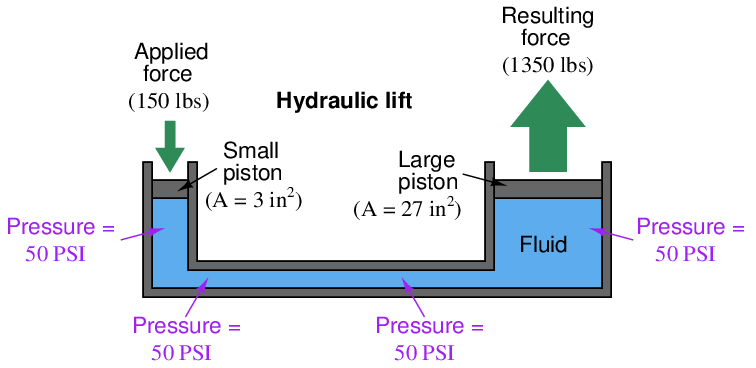
If additional force is applied to the small piston (say, 160 lbs instead of 150 lbs), the fluid pressure throughout the system will increase, not just the fluid pressure in the vicinity of the piston. The effect of this additional force will be immediately62 “felt” at all points of the system. The phenomenon of pressure changes being evenly distributed throughout an enclosed fluid is called Pascal’s principle.
Pascal’s principle is really nothing more than the direct consequence of fluids’ ability to flow. The only way an additional applied pressure would not be transmitted to all points within a confined fluid volume is if the fluid molecules were somehow not free to move. Since they are mobile, any compression applied to one region of that fluid will propagate to all other regions within that fluid volume. As fluid molecules are subjected to greater pressure, they naturally try to migrate to regions of lower pressure where they “bump up” against other fluid molecules, distributing that increased pressure in doing so.
Pascal’s principle tells us any change in applied pressure to a confined fluid will be distributed evenly throughout, but it does not say pressure will be the same throughout all points. If forces other than those applied to pistons exert pressure on the fluid, we may indeed experience gradients of pressure throughout a confined fluid volume.
In cases where we are dealing with tall columns of dense fluid, there is another force we must consider: the weight of the fluid itself. Suppose we took a cubic foot of water which weighs approximately 62.4 pounds, and poured it into a very tall vertical tube with a cross-sectional area of 1 square inch:
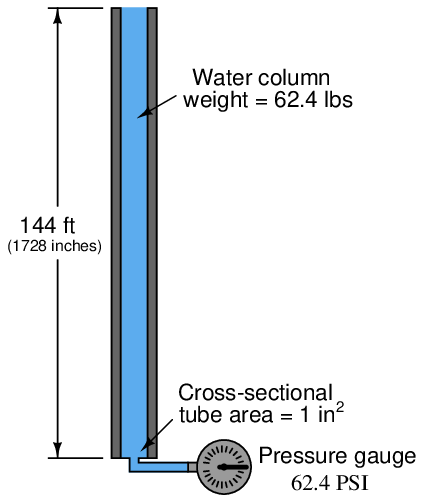
Naturally, we would expect the pressure measured at the bottom of this tall tube to be 62.4 pounds per square inch63 , since the entire column of water (weighing 62.4 pounds) has its weight supported by one square inch of area.
If we placed another pressure gauge mid-way up the tube, though, how much pressure would it register? At first you might be inclined to say 62.4 PSI as well, because you learned earlier in this lesson that fluids naturally distribute force throughout their bulk. However, in this case the pressure is not the same mid-way up the column as it is at the bottom:
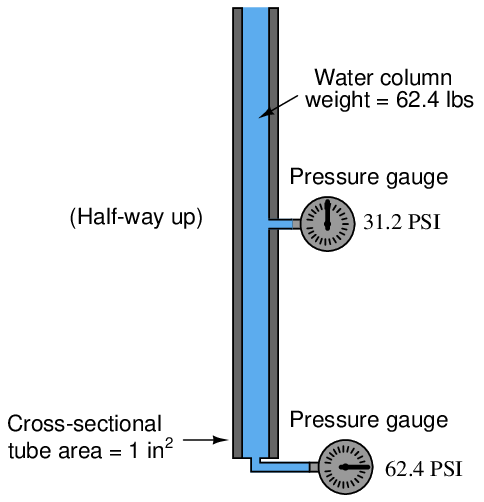
The reason for this apparent discrepancy is that the source of pressure in this fluid system comes from the weight of the water column itself. Half-way up the column, the water only experiences half the total weight (31.2 pounds), and so the pressure is half of what it is at the very bottom. We did not consider this effect before, because we assumed the force exerted by the piston in the hydraulic lift was so large it “swamped” the weight of the fluid itself. Here, with our very tall column of water (144 feet tall!), the effect of gravity upon the water’s mass is quite substantial. Indeed, without a piston to exert an external force on the water, weight is the only source of force we have to consider when calculating pressure.
This fact does not invalidate Pascal’s principle. Any change in pressure applied to the fluid column will still be distributed equally throughout. For example, if we were to place a piston at the top of this fluid column and apply a force to the fluid, pressure at all points in that fluid column would increase by the same amount64 . This is not the same as saying all pressures will be equal throughout the column, however.
An interesting fact about pressure generated by a column of fluid is that the width or shape of the containing vessel is irrelevant: the height of the fluid column is the only dimension we need to consider. Examine the following tube shapes, all connected at the bottom:
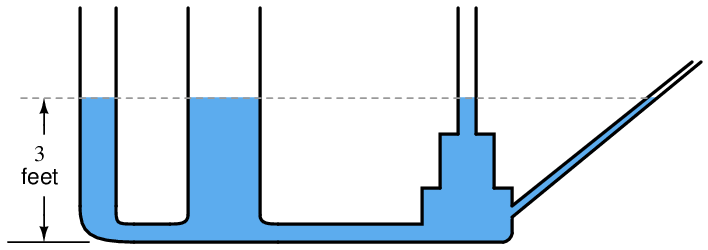
Since the force of fluid weight is generated only along the axis of gravitational attraction (straight down), that is the only axis of measurement important in determining “hydrostatic” fluid pressure.
The fixed relationship between the vertical height of a water column and pressure is such that sometimes water column height is used as a unit of measurement for pressure. That is, instead of saying “30 PSI,” we could just as correctly quantify that same pressure as 830.4 inches of water (”W.C. or ”H2O), the conversion factor being approximately 27.68 inches of vertical water column per PSI.
As one might guess, the density of the fluid in a vertical column has a significant impact on the hydrostatic pressure that column generates. A liquid twice as dense as water, for example, will produce twice the pressure for a given column height. For example, a column of this liquid (twice as dense as water) 14 inches high will produce a pressure at the bottom equal to 28 inches of water (28 ”W.C.), or just over 1 PSI. An extreme example is liquid mercury, which is over 13.5 times as dense as water. Due to its exceptional density and ready availability, the height of a mercury column is also used as a standard unit of pressure measurement. For instance, 25 PSI could be expressed as 50.9 inches of mercury (”Hg), the conversion factor being approximately 2.036 inches of vertical mercury column per PSI.
The mathematical relationship between vertical liquid height and hydrostatic pressure is quite simple, and may be expressed by either of the following formulae:
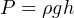
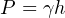
Where,
P = Hydrostatic pressure in units of weight per square area unit: pascals (N/m2) or lb/ft2
ρ = Mass density of liquid in kilograms per cubic meter (metric) or slugs per cubic foot (British)
g = Acceleration of gravity (9.81 meters per second squared or 32.2 feet per second squared)
γ = Weight density of liquid in newtons per cubic meter (metric) or pounds per cubic foot (British)
h = Vertical height of liquid column
Dimensional analysis – where we account for all units of measurement in a formula – validates the mathematical relationship between pressure, density, and height. Taking the second formula as an example:
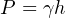
![[ ] [ ][ ]
-lb- = lb-- ft
ft2 ft3 1](https://www.technocrazed.com/books/Instrumentation/Book_half322x.png)
As you can see, the unit of “feet” in the height term cancels out one of the “feet” units in the denominator of the density term, leaving an answer for pressure in units of pounds per square foot. If one wished to set up the problem so the answer presented in a more common pressure unit such as pounds per square inch, both the liquid density and height would have to be expressed in appropriate units (pounds per cubic inch and inches, respectively).
Applying this to a realistic problem, consider the case of a tank filled with 8 feet (vertical) of castor oil, having a weight density of 60.5 pounds per cubic foot:
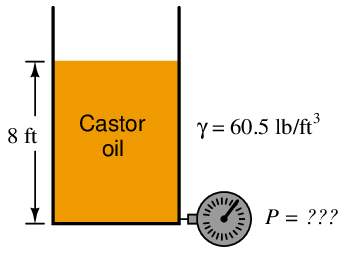
This is how we would set up the formula to calculate for hydrostatic pressure at the bottom of the tank:
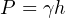
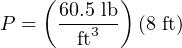
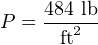
If we wished to convert this result into a more common unit such as PSI (pounds per square inch), we could do so using an appropriate fraction of conversion units:
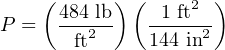
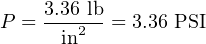
2.11.3 Fluid density expressions
The density of any substance is defined as the ratio of its mass or weight to the volume occupied by that mass or weight. Common expressions of density include pounds per cubic foot (British units) and kilograms per cubic meter (metric units). When the substance in question is a liquid, a common form of expression for density is a ratio of the liquid’s density to the density of pure water at standard temperature65 . This ratio is known as specific gravity. For example, the specific gravity of glycerin may be determined by dividing the density of glycerin by the density of water:
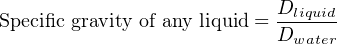
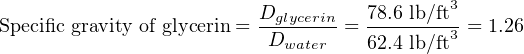
The density of gases may also be expressed in ratio form, except the standard of comparison is ambient air instead of water. Chlorine gas, for example, has a specific gravity of 2.47 (each volumetric unit of chlorine having 2.47 times the mass of the same volume of air under identical temperature and pressure conditions). Specific gravity values for gases are sometimes called relative gas densities to avoid confusion with “specific gravity” values for liquids.
As with all ratios, specific gravity is a unitless quantity. In our example with glycerine, we see how the identical units of pounds per cubic foot cancel out of both numerator and denominator, to leave a quotient with no unit at all.
An alternative to expressing fluid density as a ratio of mass (or weight) to volume, or to compare it against the density of a standard fluid such as pure water or air, is to express it as the ratio of volume to mass. This is most commonly applied to vapors such as steam, and it is called specific volume. The relationship between specific volume and density is one of mathematical reciprocation: the reciprocal of density (e.g. pounds per cubic foot) is specific volume (e.g. cubic feet per pound). For example, consulting a table of saturated steam properties, we see that saturated steam at a pressure of 60 PSIA has a specific volume of 7.175 cubic feet per pound. Translating this into units of pounds per cubic feet, we reciprocate the value 7.175 to arrive at 0.1394 pounds per cubic foot.
Industry-specific units of measurement also exist for expressing the relative density of a fluid. These units of measurement all begin with the word “degree” much the same as for units of temperature measurement, for example:
- Degrees API (used in the petroleum industries)
- Degrees Baumé (used in a variety of industries including paper manufacture and alcohol production)
- Degrees Twaddell (used in the textile industry for tanning solutions and the like)
The mathematical relationships between each of these “degree” units of density versus specific gravity66 is as follows:
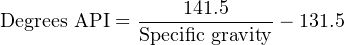
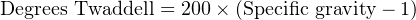
Two different formulae exist for the calculation of degrees Baumé, depending on whether the liquid in question is heavier or lighter than water. For lighter-than-water liquids:
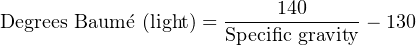
Note that pure water would measure 10o Baumé on the light scale. As liquid density decreases, the light Baumé value increases. For heavier-than-water liquids:
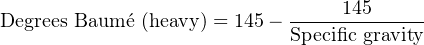
Note that pure water would measure 0o Baumé on the heavy scale. As liquid density increases, the heavy Baumé value increases.
Just to make things confusing, there are different standards for the heavy Baumé scale. Instead of the constant value 145 shown in the above equation (used throughout the United States of America), an older Dutch standard used the same formula with a constant value of 144. The Gerlach heavy Baumé scale uses a constant value of 146.78:
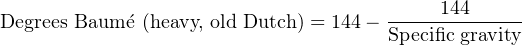
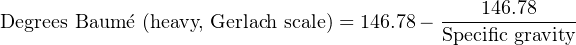
There exists a seemingly endless array of “degree” scales used to express liquid density, scattered throughout the pages of history. For the measurement of sugar concentrations in the food industries, the unit of degrees Balling was invented. This scale was later revised to become the unit of degrees Brix, which is directly proportional to the percent concentration of sugar in the liquid. Another density scale used for expressing sugar concentration is degrees Plato. The density of tanning liquor may be measured in degrees Bark. Milk density may be measured in degrees Soxhlet. Vegetable oil density (and in older times, the density of oil extracted from sperm whales) may be measured in degrees Oleo.
2.11.4 Manometers
Expressing fluid pressure in terms of a vertical liquid column makes perfect sense when we use a very simple kind of motion-balance pressure instrument called a manometer. A manometer is nothing more than a piece of clear (glass or plastic) tubing filled with a liquid of known density, situated next to a scale for measuring distance. The most basic form of manometer is the U-tube manometer, shown here:
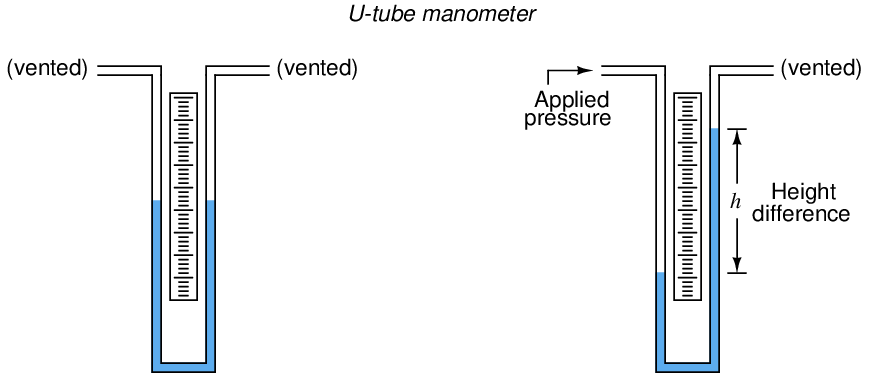
The basis for all manometers is the mathematical relationship between a liquid’s density (ρ in mass units or γ in weight units) and vertical height. The diameter of the manometer tubes is irrelevant:
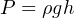
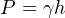
Pressure is read on the scale as the difference in height (h) between the two liquid columns. One nice feature of a manometer is it really cannot become “uncalibrated” so long as the fluid is pure and the assembly is maintained in an upright position. If the fluid used is water, the manometer may be filled and emptied at will, and even rolled up for storage if the tubes are made of flexible plastic.
We may create even more sensitive manometers by purposely inclining one or more of the tubes, so that the liquid must travel a farther distance along the tube length to achieve the same vertical shift in height. This has the effect of “amplifying” the liquid’s motion to make it easier to resolve small pressures:
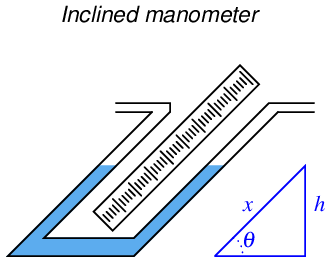
This way, a greater motion of liquid (x) is required to generate the same hydrostatic pressure (vertical liquid displacement, h) than in an upright manometer, making the inclined manometer more sensitive. As the similar triangle in the illustration shows, x and h are related trigonometrically by the sine function:
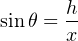
The difference in fluid column positions measured diagonally along the scale (x) must always be greater than the vertical height difference between the two columns (h) by a factor of 1 __ sin θ, which will always be greater than one for angles less than 90o. The smaller the angle θ, the greater the ratio between x and h, leading to more sensitivity.
If even more sensitivity is desired, we may construct something called a micromanometer, consisting of a gas bubble trapped in a clear horizontal tube between two large vertical manometer chambers:
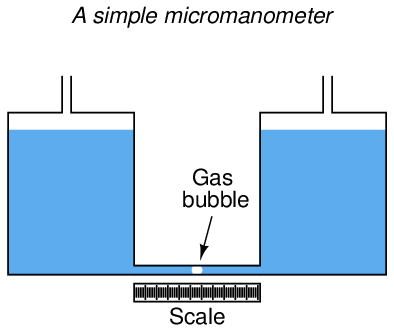
Pressure applied to the top of either vertical chamber will cause the vertical liquid columns to shift just the same as any U-tube manometer. However, the bubble trapped in the clear horizontal tube will move much farther than the vertical displacement of either liquid column, owing to the huge difference in cross-sectional area between the vertical chambers and the horizontal tube. This amplification of motion is analogous to the amplification of motion in a hydraulic piston system (where the smaller piston moves farther than the larger piston), and makes the micromanometer exceptionally sensitive to small pressures.
The movement of the gas bubble within the clear horizontal viewing tube (x) relates to applied pressure by the following formula:
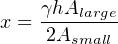
Using water as the working liquid in a standard U-tube manometer, 1 PSI of applied gas pressure results in approximately 27.7 inches of vertical liquid column displacement (i.e. 27.7 inches of height difference between the two water columns). This relatively large range of motion limits the usefulness of water manometers to modest pressures only. If we wished to use a water manometer to measure the pressure of compressed air in an industrial pneumatic supply system at approximately 100 PSI, the manometer would have to be in excess of 230 feet tall! Clearly, a water manometer would not be the proper instrument to use for such an application.
However, water is not the only viable liquid for use in manometers. We could take the exact same clear U-tube and fill it partially full of liquid mercury instead, which is substantially denser than water. In a mercury manometer, 1 PSI of applied gas pressure results in very slightly more than 2 inches of liquid column displacement. A mercury manometer applied to the task of measuring air pressure in an industrial pneumatic system would only have to be 17 feet tall – still quite large and cumbersome67 for a measuring instrument, but not impossible to construct or to use.
A common form of manometer seen in industrial instrument calibration shops is the well type, consisting of a single vertical tube and a relatively large reservoir (called the “well”) acting as the second column:
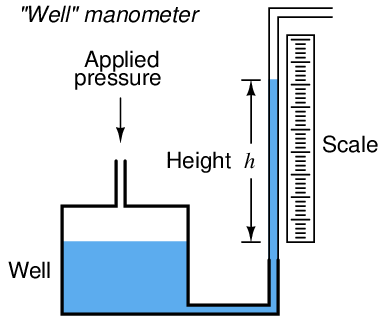
Due to the well’s much larger cross-sectional area, liquid motion inside of it is negligible compared to the motion of liquid inside the clear viewing tube. For all practical purposes68 , the liquid level inside the “well” is constant, and so the liquid inside the tube moves the full distance equivalent to the applied pressure. Thus, the well manometer provides an easier means of reading pressure: no longer does one have to measure the difference of height between two liquid columns, only the height of a single column.
2.11.5 Systems of pressure measurement
Pressure measurement is often a relative thing. When we say there is 35 PSI of air pressure in an inflated car tire, what we mean is that the pressure inside the tire is 35 pounds per square inch greater than the surrounding, ambient air pressure. It is a fact that we live and breathe in a pressurized environment. Just as a vertical column of liquid generates a hydrostatic pressure, so does a vertical column of gas. If the column of gas is very tall, the pressure generated by it will be substantial. Such is the case with Earth’s atmosphere, the pressure at sea level caused by the weight of the atmosphere being approximately 14.7 PSI.
You and I do not perceive this constant air pressure around us because the pressure inside our bodies is equal to the pressure outside our bodies. Thus our eardrums, which serve as differential pressure-sensing diaphragms, detect no difference of pressure between the inside and outside of our bodies. The only time the Earth’s air pressure becomes perceptible to us is if we rapidly ascend or descend, where the pressure inside our bodies does not have time to equalize with the pressure outside, and we feel the force of that differential pressure on our eardrums.
If we wish to speak of a fluid pressure in terms of how it compares to a perfect vacuum (absolute zero pressure), we specify it in terms of absolute units. For example, when I said earlier that the atmospheric pressure at sea level was 14.7 PSI, what I really meant is it is 14.7 PSIA (pounds per square inch absolute), meaning 14.7 pounds per square inch greater than a perfect vacuum. When I said earlier that the air pressure inside an inflated car tire was 35 PSI, what I really meant is it was 35 PSIG (pounds per square inch gauge), meaning 35 pounds per square inch greater than ambient air pressure. The qualifier “gauge” implies the pressure indicated by a pressure-measuring gauge, which in most cases works by comparing the sample fluid’s pressure to that of the surrounding atmosphere. When units of pressure measurement are specified without a “G” or “A” suffix, “gauge” pressure is usually69 assumed.
Gauge and absolute pressure values for some common fluid pressures are shown in this table:

Note that the only difference between each of the corresponding gauge and absolute pressures is an offset of 14.7 PSI, with absolute pressure being the larger (more positive) value.
This offset of 14.7 PSI between absolute and gauge pressures can be confusing if we must convert between different pressure units. Suppose we wished to express the tire pressure of 35 PSIG in units of inches of water column (”W.C.). If we stay in the gauge-pressure scale, all we have to do is multiply by 27.68:
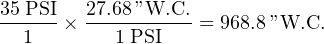
Note how the fractions have been arranged to facilitate cancellation of units. The “PSI” unit in the numerator of the first fraction cancels with the “PSI” unit in the denominator of the second fraction, leaving inches of water column (”W.C.) as the only unit standing. Multiplying the first fraction (35 PSI over 1) by the second fraction (27.68 ”W.C. over 1 PSI) is “legal” to do since the second fraction has a physical value of unity (1): being that 27.68 inches of water column is the same physical pressure as 1 PSI, the second fraction is really the number “1” in disguise. As we know, multiplying any quantity by unity does not change its value, so the result of 968.8 ”W.C. we get has the exact same physical meaning as the original figure of 35 PSI. This technique of unit conversion is sometimes known as unity fractions, and it is discussed in more general terms in another section of this book.
If, however, we wished to express the car’s tire pressure in terms of inches of water column absolute (in reference to a perfect vacuum), we would have to include the 14.7 PSI offset in our calculation, and do the conversion in two steps:
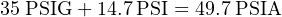
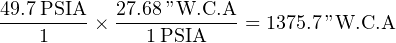
The ratio between inches of water column and pounds per square inch is still the same (27.68:1) in the absolute scale as it is in the gauge scale. The only difference is that we included the 14.7 PSI offset in the very beginning to express the tire’s pressure on the absolute scale rather than on the gauge scale. From then on, all conversions were performed in absolute units.
This two-step conversion process is not unlike converting between different units of temperature (degrees Celsius versus degrees Fahrenheit), and for the exact same reason. To convert from oF to oC, we must first subtract an offset of 32 degrees, then multiply by 5 9. The reason an offset is involved in this temperature conversion is because the two temperature scales do not share the same “zero” point: 0 oC is not the same temperature as 0 oF. Likewise, 0 PSIG is not the same pressure as 0 PSIA, and so an offset is always necessary to convert between gauge and absolute pressure units.
As seen with the unit of pounds per square inch (PSI), the distinction between gauge and absolute pressure is typically shown by a lettered suffix “G” or “A” following the unit, respectively. Following this convention, we may encounter other units of pressure measurement qualified as either gauge or absolute by these letters: kPaA (kilopascals absolute), inches HgG (inches of mercury gauge), inches W.C.A (inches of water column absolute), etc.
There are some pressure units that are always in absolute terms, and as such require no letter “A” to specify. One is the unit of atmospheres, 1 atmosphere being 14.7 PSIA. There is no such thing as “atmospheres gauge” pressure. For example, if we were given a pressure as being 4.5 atmospheres and we wanted to convert that into pounds per square inch gauge (PSIG), the conversion would be a two-step process:
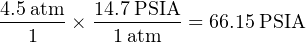
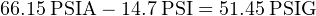
Another unit of pressure measurement that is always absolute is the torr, equal to 1 millimeter of mercury column absolute (mmHgA). 0 torr is absolute zero, equal to 0 atmospheres, 0 PSIA, or −14.7 PSIG. Atmospheric pressure at sea level is 760 torr, equal to 1 atmosphere, 14.7 PSIA, or 0 PSIG.
If we wished to convert the car tire’s pressure of 35 PSIG into torr, we would once again have to offset the initial value to get everything into absolute terms.
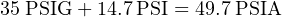
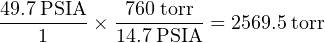
One last unit of pressure measurement deserves special comment, for it may be used to express either gauge or absolute pressure, yet it is not customary to append a “G” or an “A” to the unit. This unit is the bar, exactly equal to 100 kPa, and approximately equal70 to 14.5 PSI. Some technical references append a lower-case letter “g” or “a” to the word “bar” to show either gauge pressure (barg) or absolute pressure (bara), but this notation seems no longer favored. Modern usage typically omits the “g” or “a” suffix in favor of context: the word “gauge” or “absolute” may be included in the expression to clarify the meaning of “bar.” Sadly, many references fail to explicitly declare either “gauge” or “absolute” when using units of bar, leaving the reader to interpret the intended context. Despite this ambiguity, the bar is frequently used in European literature as a unit of pressure measurement.
2.11.6 Negative pressure
If a chamber is completely evacuated of any and all fluid molecules such that it contains nothing but empty space, we say that it contains a perfect vacuum. With no fluid molecules inside the chamber whatsoever, there will be no pressure exerted on the chamber walls by any fluid. This is the defining condition of zero absolute pressure (e.g. 0 PSIA, 0 torr, 0 atmospheres, etc.). Referencing atmospheric air pressure71 outside of this vessel, we could say that the “gauge” pressure of a perfect vacuum is −14.7 PSIG.
A commonly-taught principle is that a perfect vacuum is the lowest pressure possible in any physical system. However, this is not strictly true. It is, in fact, possible to generate pressures below 0 PSIA – pressures that are actually less than that of a perfect vacuum. The key to understanding this is to consider non-gaseous systems, where the pressure in question exists within a solid or a liquid substance.
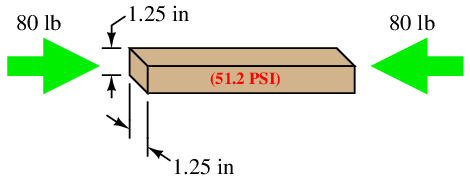
Let us begin our exploration of this concept by considering the case of weight applied to a solid metal bar:

Recall that pressure is defined as force exerted over area. This metal bar certainly has a cross-sectional area, and if a compressive force is applied to the bar then the molecules of metal inside the bar will experience a pressure attempting to force them closer together. Supposing the bar in question measured 1.25 inches wide and thick, its cross-sectional area would be (1.25 in)2, or 1.5625 in2. Applying a force of 80 pounds along the bar’s length would set up an internal pressure within the bar of 51.2 pounds per square inch, or 51.2 PSI:
Now suppose we reverse the direction of the applied force to the bar, applying tension to the bar rather than compression. If the force is still 80 pounds and the cross-sectional area is still 1.5625 square inches, then the internal pressure inside the bar must be −51.2 PSI:
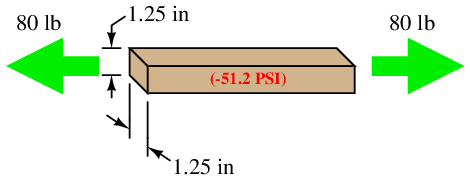
The negative pressure value describes the tensile force experienced by the molecules of metal inside the bar: a degree of force per unit area attempting to pull those molecules apart from each other rather than push them closer together as was the case with a compressive force.
If you believe that the lowest possible pressure is a perfect vacuum (0 PSIA, or −14.7 PSIG), then this figure of −51.2 PSI seems impossible. However, it is indeed possible because we are dealing with a solid rather than with a gas. Gas molecules exert pressure on a surface by striking that surface and exerting a force by the momentum of their impact. Since gas molecules can only strike (i.e. push) against a surface, and cannot pull against a surface, one cannot generate a negative absolute pressure using a gas. In solids, however, the molecules comprising the sample exhibit cohesion, allowing us to set up a tension within that material impossible in a gaseous sample where there is no cohesion between the molecules. Thus, negative pressures are possible within samples of solid material even though they are impossible within gases.
Negative pressures are also possible within liquid samples, provided there are no bubbles of gas or vapor anywhere within the sample. Like solids, the molecules within a liquid also exhibit cohesion (i.e. they tend to “stick” together rather than drift apart from each other). If a piston-and-cylinder arrangement is completely filled with liquid, and a tension applied to the movable piston, the molecules within that liquid will experience tension as well. Thus, it is possible to generate negative pressures (below 0 PSIA) within liquids that are impossible with gases.
Even vertical columns of liquid may generate negative pressure. The famous British scientists Hooke and Boyle demonstrated a negative pressure of −0.2 MPa (−29 PSI) using a column of liquid mercury. Trees naturally generate huge negative pressures in order to draw water to their full height, up from the ground. Two scientists, H.H. Dixon and J. Joly, presented a scientific paper entitled On the Ascent of Sap in 1895 proposing liquid tension as the mechanism by which trees could draw water up tremendous heights.
If even the smallest bubble of gas exists within a liquid sample, however, negative pressures become impossible. Since gases can only exert positive pressures, and Pascal’s Principle tells us that pressure will be equally distributed throughout a fluid sample, the low-limit of 0 PSIA for gases establishes a low pressure limit for the entire liquid/gas sample. In other words, the presence of any gas within an otherwise liquid sample prevents the entire sample from experiencing tension.
One limitation to the generation of negative pressures within liquids is that disturbances and/or impurities within the liquid may cause that liquid to spontaneously boil (changing phase from liquid to vapor), at which point a sustained negative pressure becomes impossible.
2.11.7 Buoyancy
When a solid body is immersed in a fluid, it displaces an equal volume of that fluid. This displacement of fluid generates an upward force on the object called the buoyant force. The magnitude of this force is equal to the weight of the fluid displaced by the solid body, and it is always directed exactly opposite the line of gravitational attraction. This is known as Archimedes’ Principle.
Buoyant force is what makes ships float. A ship sinks into the water just enough so the weight of the water displaced is equal to the total weight of the ship and all it holds (cargo, crew, food, fuel, etc.):
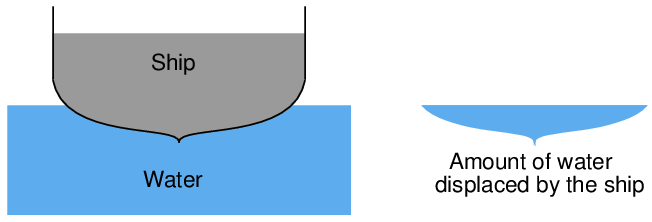
If we could somehow measure the weight of that water displaced, we would find it exactly equals the dry weight of the ship:
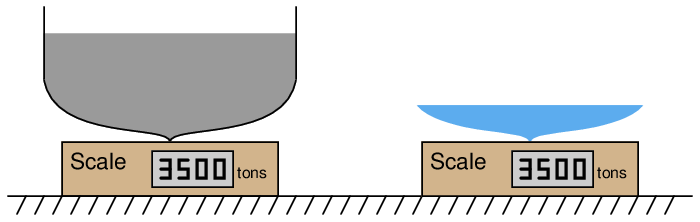
Expressed mathematically, Archimedes’ Principle states that the buoyant force is the product of the liquid volume and liquid density:
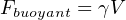
Where,
Fb = Buoyant force exerted on object, opposite in direction from gravity
γ = Weight density of liquid
V = Volume of liquid displaced by the submerged object
We may use dimensional analysis to confirm correct cancellation of British units in the Archimedes’ Principle formula:
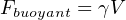
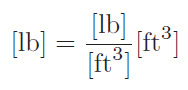
Notice how the units of measurement for weight density (pounds per cubic foot) combine with the unit of measurement for volume (cubic feet) to cancel the unit of cubic feet and leave us with force measured in pounds.
Archimedes’ Principle also explains why hot-air balloons and helium aircraft float. By filling a large enclosure with a gas that is less dense than the surrounding air, that enclosure experiences an upward (buoyant) force equal to the difference between the weight of the air displaced and the weight of the gas enclosed. If this buoyant force equals the weight of the craft and all it holds (cargo, crew, food, fuel, etc.), it will exhibit an apparent weight of zero, which means it will float. If the buoyant force exceeds the weight of the craft, the resultant force will cause an upward acceleration according to Newton’s Second Law of motion (F = ma).
Submarines also make use of Archimedes’ Principle, adjusting their buoyancy by adjusting the amount of water held by ballast tanks on the hull. Positive buoyancy is achieved by “blowing” water out of the ballast tanks with high-pressure compressed air, so the submarine weighs less (but still occupies the same hull volume and therefore displaces the same amount of water). Negative buoyancy is achieved by “flooding” the ballast tanks so the submarine weighs more. Neutral buoyancy is when the buoyant force exactly equals the weight of the submarine and the remaining water stored in the ballast tanks, so the submarine is able to “hover” in the water with no vertical acceleration or deceleration.
An interesting application of Archimedes’ Principle is the quantitative determination of an object’s density by submersion in a liquid. For instance, copper is 8.96 times as dense as water, with a mass of 8.96 grams per cubic centimeter (8.96 g/cm3) as opposed to water at 1.00 gram per cubic centimeter (1.00 g/cm3). If we had a sample of pure, solid copper exactly 1 cubic centimeter in volume, it would have a mass of 8.96 grams. Completely submerged in pure water, this same sample of solid copper would appear to have a mass of only 7.96 grams, because it would experience a buoyant force equivalent to the mass of water it displaces (1 cubic centimeter = 1 gram of water). Thus, we see that the difference between the dry mass (mass measured in air) and the wet mass (mass measured when completely submerged in water) is the mass of the water displaced. Dividing the sample’s dry mass by this mass difference (dry − wet mass) yields the ratio between the sample’s mass and the mass of an equivalent volume of water, which is the very definition of specific gravity. The same calculation yields a quantity for specific gravity if weights instead of masses are used, since weight is nothing more than mass multiplied by the acceleration of gravity (Fweight = mg), and the constant g cancels out of both numerator and denominator:
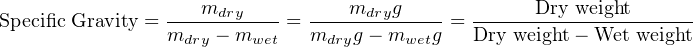
Another application of Archimedes’ Principle is the use of a hydrometer for measuring liquid density. If a narrow cylinder of precisely known volume and weight (most of the weight concentrated at one end) is immersed in liquid, that cylinder will sink to a level dependent on the liquid’s density. In other words, it will sink to a level sufficient to displace its own weight in fluid. Calibrated marks made along the cylinder’s length may then serve to register liquid density in any unit desired.
A simple style of hydrometer used to measure the density of lead-acid battery electrolyte is shown in this illustration:
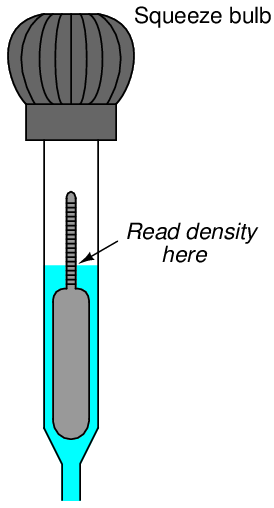
To use this hydrometer, you must squeeze the rubber bulb at the top and dip the open end of the tube into the liquid to be sampled. Relaxing the rubber bulb will draw a sample of liquid up into the tube where it immerses the float. When enough liquid has been drawn into the tube to suspend the float so that it neither rests on the bottom of the tapered glass tube or “tops out” near the bulb, the liquid’s density may be read at the air/liquid interface.
A denser electrolyte liquid results in the float rising to a higher level inside the hydrometer tube:
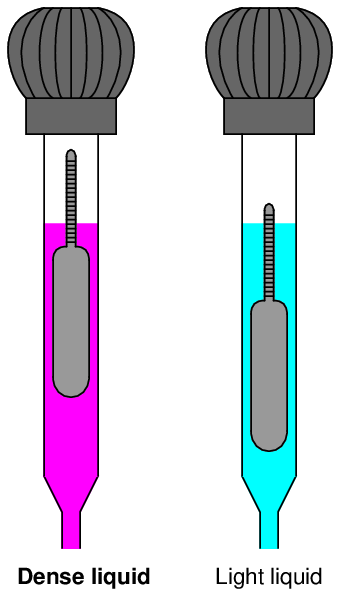
Like all floating objects, the hydrometer float naturally seeks a condition of neutral buoyancy where the weight of the displaced liquid exactly equals the dry weight of the float. If the liquid happens to be very dense, the float will not have to sink very far in order to achieve neutral buoyancy; the less dense the liquid, the deeper the float must sink in order to achieve neutral buoyancy.
This means the float’s graduated density scale will read less density toward the top and greater density toward the bottom.
The following photograph shows a set of antique hydrometers used to measure the density of beer. The middle hydrometer bears a label showing its calibration to be in degrees Baumé (heavy):

Liquid density measurement is useful in the alcoholic beverage industry to infer alcohol content. Since alcohol is less dense than water, a sample containing a greater concentration of alcohol (a greater proof rating) will be less dense than a “weaker” sample, all other factors being equal.
A less sophisticated version of hydrometer uses multiple balls of differing density. A common application for such a hydrometer is measuring the concentration of “antifreeze” coolant for automobile engines, comprised of a mixture of ethylene glycol and water. Ethylene glycol is a denser compound than water, and so a “stronger” mixture of antifreeze will have a greater bulk density than a “weaker” density of antifreeze. This style of hydrometer yields a crude measurement of ethylene glycol concentration based on the number of balls that float:

A greater number of floating balls represents a “stronger” concentration of glycol in the coolant. “Weak” glycol concentrations represent a greater percentage of water in the coolant, with a correspondingly higher freezing temperature.
Similar hydrometers are used to measure the concentration of sulfuric acid in lead-acid battery electrolyte, comprised of acid and water. The more fully charged a lead-acid battery is, the higher the concentration of sulfuric acid in the electrolyte fluid. The more discharged a lead-acid battery becomes, the less sulfuric acid (and the more water) is present in the electrolyte. Since sulfuric acid is a denser compound than water, measuring electrolyte density with a hydrometer yields a crude measurement of battery charge state.
2.11.8 Gas Laws
The Ideal Gas Law relates pressure, volume, molecular quantity, and temperature of an ideal gas together in one concise mathematical expression:
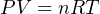
Where,
P = Absolute pressure (atmospheres)
V = Volume (liters)
n = Gas quantity (moles)
R = Universal72 gas constant (0.0821 L ⋅ atm / mol ⋅ K)
T = Absolute temperature (K)
For example, the Ideal Gas Law predicts five moles of helium gas (20 grams worth) at a pressure of 1.4 atmospheres and a temperature of 310 Kelvin will occupy 90.9 liters of volume.
An alternative form of the Ideal Gas Law uses the number of actual gas molecules (N) instead of the number of moles of molecules (n):
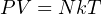
Where,
P = Absolute pressure (Pascals)
V = Volume (cubic meters)
N = Gas quantity (molecules)
k = Boltzmann’s constant (1.38 × 10−23 J / K)
T = Absolute temperature (K)
Interestingly, the Ideal Gas Law holds true for any gas. The theory behind this assumption is that gases are mostly empty space: there is far more volume of empty space separating individual gas molecules in a sample than there is space occupied by the gas molecules themselves. This means variations in the sizes of individual gas molecules within any sample is negligible, and therefore the type of gas molecules contained within the sample is irrelevant. Thus, we may apply either form of the Ideal Gas Law to situations regardless of the type of gas involved. This is also why the Ideal Gas Law does not apply to liquids or to phase changes (e.g. liquids boiling into gas): only in the gaseous phase will you find individual molecules separated by relatively large distances.
To modify the previous example, where 5 moles of helium gas occupied 90.9 liters at 1.4 atmospheres and 310 Kelvin, it is also true that 5 moles of nitrogen gas will occupy the same volume (90.9 liters) at 1.4 atmospheres and 310 Kelvin. The only difference will be the mass of each gas sample. 5 moles of helium gas (4He) will have a mass of 20 grams, whereas 5 moles of nitrogen gas (14N2) will have a mass of 140 grams.
Although no gas in real life is ideal, the Ideal Gas Law is a close approximation for conditions of modest gas density, and no phase changes (gas turning into liquid or vice-versa). You will find this Law appearing again and again in calculations of gas volume and gas flow rates, where engineers and technicians must know the relationship between gas volume, pressure, and temperature.
Since the molecular quantity of an enclosed gas is constant, and the universal gas constant must be constant, the Ideal Gas Law may be written as a proportionality instead of an equation:
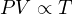
Several “gas laws” are derived from this proportionality. They are as follows:
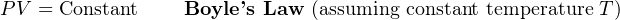
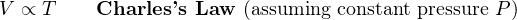
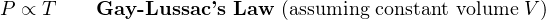
You will see these laws referenced in explanations where the specified quantity is constant (or very nearly constant).
For non-ideal conditions, the “Real” Gas Law formula incorporates a corrected term for the compressibility of the gas:
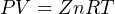
Where,
P = Absolute pressure (atmospheres)
V = Volume (liters)
Z = Gas compressibility factor (unitless)
n = Gas quantity (moles)
R = Universal gas constant (0.0821 L ⋅ atm / mol ⋅ K)
T = Absolute temperature (K)
The compressibility factor for an ideal gas is unity (Z = 1), making the Ideal Gas Law a limiting case of the Real Gas Law. Real gases have compressibility factors less than unity (< 1). What this means is real gases tend to compress more than the Ideal Gas Law would predict (i.e. occupies less volume for a given amount of pressure than predicted, and/or exerts less pressure for a given volume than predicted).
2.11.9 Fluid viscosity
Viscosity is a measure of a fluid’s resistance to shear. It may be visualized as a sort of internal friction, where individual fluid molecules experience either cohesion or collision while flowing past one another. The more “viscous” a fluid is, the “thicker” it is when stirred. Clean water is an example of a low-viscosity liquid, while liquid honey at room temperature is an example of a high-viscosity liquid.
There are two different ways to quantify the viscosity of a fluid: absolute viscosity and kinematic viscosity. Absolute viscosity (symbolized by the Greek symbol “eta” η, or sometimes by the Greek symbol “mu” μ), also known as dynamic viscosity, is a direct relation between stress placed on a fluid and its rate of deformation (or shear). The textbook definition of absolute viscosity is based on a model of two flat plates moving past each other with a film of fluid separating them. The relationship between the shear stress applied to this fluid film (force divided by area) and the velocity/film thickness ratio is viscosity:

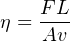
Where,
η = Absolute viscosity (pascal-seconds), also symbolized as μ
F = Force (newtons)
L = Film thickness (meters) – typically much less than 1 meter for any realistic demonstration!
A = Plate area (square meters)
v = Relative velocity (meters per second)
Another common unit of measurement for absolute viscosity is the poise, with 1 poise being equal to 0.1 pascal-seconds. Both units are too large for common use, and so absolute viscosity is often expressed in centipoise. Water has an absolute viscosity of very nearly 1.000 centipoise.
Kinematic viscosity (symbolized by the Greek letter “nu” ν) includes an assessment of the fluid’s density in addition to all the above factors. It is calculated as the quotient of absolute viscosity and mass density:
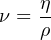
Where,
ν = Kinematic viscosity (stokes)
η = Absolute viscosity (poise)
ρ = Mass density (grams per cubic centimeter)
As with the unit of poise, the unit of stokes is too large for convenient use, so kinematic viscosities are often expressed in units of centistokes. Water has a kinematic viscosity of very nearly 1.000 centistokes.
The mechanism of viscosity in liquids is inter-molecular cohesion. Since this cohesive force is overcome with increasing temperature, most liquids tend to become “thinner” (less viscous) as they heat up. The mechanism of viscosity in gases, however, is inter-molecular collisions. Since these collisions increase in frequency and intensity with increasing temperature, gases tend to become “thicker” (more viscous) as they heat up.
As a ratio of stress to strain (applied force to yielding velocity), viscosity is often constant for a given fluid at a given temperature. Interesting exceptions exist, though. Fluids whose viscosities change with applied stress, and/or over time with all other factors constant, are referred to as non-Newtonian fluids. A simple example of a non-Newtonian fluid is cornstarch mixed with water, which “solidifies” under increasing stress and then returns to a liquid state when the stress is removed.
2.11.10 Reynolds number
Viscous flow is a condition where friction forces dominate the behavior of a moving fluid, typically in cases where viscosity (internal fluid friction) is great. Inviscid flow, by contrast, is a condition where friction within a moving fluid is negligible and the fluid moves freely. The Reynolds number of a fluid is a dimensionless quantity expressing the ratio between a moving fluid’s momentum and its viscosity, and is a helpful gauge in predicting how a fluid stream will move.
A couple of formulae for calculating Reynolds number of a flow are shown here:
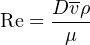
Where,
Re = Reynolds number (unitless)
D = Diameter of pipe, (meters)
v = Average velocity of fluid (meters per second)
ρ = Mass density of fluid (kilograms per cubic meter)
μ = Absolute viscosity of fluid (pascal-seconds)
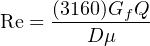
Where,
Re = Reynolds number (unitless)
Gf = Specific gravity of liquid (unitless)
Q = Flow rate (gallons per minute)
D = Diameter of pipe (inches)
μ = Absolute viscosity of fluid (centipoise)
3160 = Conversion factor for British units
The first formula, with all metric units, is the textbook “definition” for Reynolds number. If you take the time to dimensionally analyze this formula, you will find that all units do indeed cancel to leave the Reynolds number unitless:
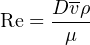
![[m-][kg]
Re = [m-]-s---m3--
[Pa ⋅s]](https://www.technocrazed.com/books/Instrumentation/Book_half379x.png)
Recalling that the definition of a “pascal” is one Newton of force per square meter:
![[ ]
kg-
Re = [m-⋅s]-
Nm2⋅s](https://www.technocrazed.com/books/Instrumentation/Book_half380x.png)
![[ ] [ ]
-kg- -m2-
Re = m ⋅s ⋅ N ⋅s](https://www.technocrazed.com/books/Instrumentation/Book_half381x.png)
![[ ]
kg⋅m-
Re = N ⋅s2](https://www.technocrazed.com/books/Instrumentation/Book_half382x.png)
Recalling that the definition of a “newton” is one kilogram times meters per second squared (from Newton’s Second Law equation F = ma):
![[ ]
Re = kg⋅m-⋅s2
kg⋅m ⋅s2](https://www.technocrazed.com/books/Instrumentation/Book_half383x.png)
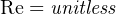
The second formula given for calculating Reynolds number includes a conversion constant of 3160, which bears the unwieldy unit of “inches-centipoise-minutes per gallon” in order that the units of all variables (flow in gallons per minute, pipe diameter in inches, and viscosity in centipoise) may cancel. Note that specific gravity (Gf) is unitless and therefore does not appear in this dimensional analysis:
[in⋅cp]
” class=”math-display”>
You will often find this formula, and the conversion constant of 3160, shown without units at all. Its sole purpose is to make the calculation of Reynolds number easy when working with British units customary in the United States.
The Reynolds number of a fluid stream may be used to qualitatively predict whether the flow regime will be laminar or turbulent. Low Reynolds number values predict laminar (viscous) flow, where fluid molecules move in straight “stream-line” paths, and fluid velocity near the center of the pipe is substantially greater than near the pipe walls:
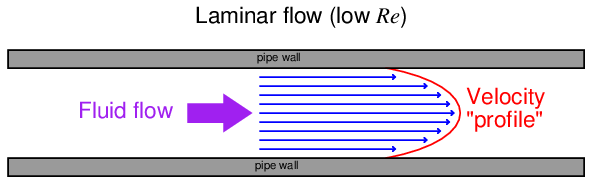
High Reynolds number values predict turbulent (inviscid) flow, where individual molecule motion is chaotic on a microscopic scale, and fluid velocities across the face of the flow profile are similar:
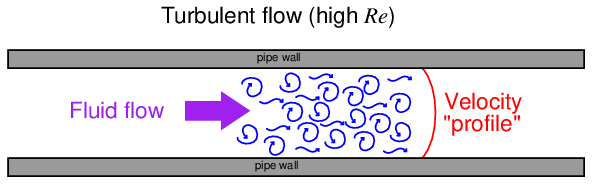
It should be emphasized that this turbulence is microscopic in nature, and occurs even when the fluid flows through a piping system free of obstructions, rough surfaces, and/or sudden directional changes. At high Reynolds number values, turbulence simply happens.
Other forms of turbulence, such as eddies and swirl are possible at high Reynolds numbers, but are caused by disturbances in the flow stream such as pipe elbows, tees, control valves, thermowells, and other irregular surfaces. The “micro-turbulence” naturally occurring at high Reynolds numbers will actually randomize such macroscopic (large-scale) motions if the fluid subsequently passes through a long enough length of straight pipe.
Turbulent flow is actually the desired condition for many industrial processes. When different fluids must be mixed together, for example, laminar flow is a bad thing: only turbulent flow will guarantee thorough mixing. The same is true for convective heat exchange: in order for two fluids to effectively exchange heat energy within a heat exchanger, the flow must be turbulent so that molecules from all portions of the flow stream will come into contact with the exchanger walls. Many types of flowmeters require a condition called fully-developed turbulent flow, where the flow profile is relatively flat and the only turbulence is that existing on a microscopic scale. Large-scale disturbances in the flow profile such as eddies and swirl tend to negatively affect the measurement performance of many flowmeter designs. This is why such flowmeters usually require long lengths of “straight-run” piping both upstream and downstream: to give micro-turbulence the opportunity to randomize any large-scale motions and homogenize the velocity profile.
A generally accepted rule-of-thumb is that Reynolds number values less than 2000 will probably be laminar, while values in excess of 10000 will probably be turbulent. There is no definite threshold value for all fluids and piping configurations, though. To illustrate, I will share with you some examples of Reynolds number thresholds for laminar versus turbulent flows given by various technical sources:
Chapter 2.8: Laminar Flowmeters of the Instrument Engineers’ Handbook, Process Measurement and Analysis, Third Edition (pg. 105 – authors: R. Siev, J.B. Arant, B.G. Lipták) define Re < 2000 as “laminar” flow, Re > 10000 as “fully developed turbulent” flow, and any Reynolds number values between 2000 and 10000 as “transitional” flow.
Chapter 2: Fluid Properties – Part II of the ISA Industrial Measurement Series – Flow (pg. 11) define “laminar” flow as Re < 2000, “turbulent” flow as Re > 4000, and any Reynolds values in between 2000 and 4000 as “transitional” flow.
The Laminar Flow in a Pipe section in the Standard Handbook of Engineering Calculations (pg. 1-202) defines “laminar” flow as Re < 2100, and “turbulent” flow as Re > 3000. In a later section of that same book (Piping and Fluid Flow – page 3-384), “laminar” flow is defined as Re < 1200 and “turbulent” flow as Re > 2500.
Douglas Giancoli, in his physics textbook Physics (third edition, pg. 11), defines “laminar” flow as Re < 2000 and “turbulent” flow as Re > 2000.
Finally, a source on the Internet (https://flow.netfirms.com/reynolds/theory.htm) attempts to define the threshold separating laminar from turbulent flow to an unprecedented degree of precision: Re < 2320 is supposedly the defining point of “laminar” flow, while Re > 2320 is supposedly marks the onset of “turbulent” flow.
Clearly, Reynolds number alone is insufficient for consistent prediction of laminar or turbulent flow, otherwise we would find far greater consistency in the reported Reynolds number values for each regime. Pipe roughness, swirl, and other factors influence flow regime, making Reynolds number an approximate indicator only. It should be noted that laminar flow may be sustained at Reynolds numbers significantly in excess of 10000 under very special circumstances. For example, in certain coiled capillary tubes, laminar flow may be sustained all the way up to Re = 15000, due to a phenomenon known as the Dean effect!
2.11.11 Law of Continuity
Any fluid moving through a pipe obeys the Law of Continuity, which states that the product of average velocity (v), pipe cross-sectional area (A), and fluid density (ρ) for a given flow stream must remain constant:
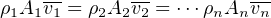
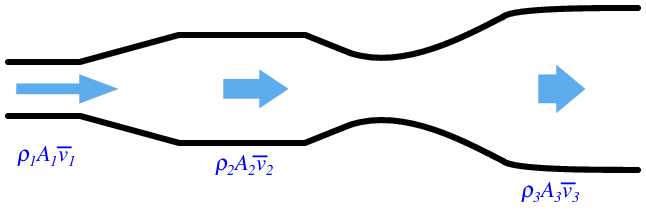
Fluid continuity is an expression of a more fundamental law of physics: the Conservation of Mass. If we assign appropriate units of measurement to the variables in the continuity equation, we see that the units cancel in such a way that only units of mass per unit time remain:
![[ kg] [m2 ][m ] [kg ]
ρAv-= -3- --- -- = --
m 1 s s](https://www.technocrazed.com/books/Instrumentation/Book_half392x.png)
This means we may define the product ρAv as an expression of mass flow rate, or W:
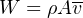
In order for the product ρAv to differ between any two points in a pipe, mass would have to mysteriously appear and disappear. So long as the flow is continuous (not pulsing), and the pipe does not leak, it is impossible to have different rates of mass flow at different points along the flow path without violating the Law of Mass Conservation. The continuity principle for fluid through a pipe is analogous to the principle of current being the same everywhere in a series-connected electric circuit, and for equivalently the same reason73 .
We refer to a flowing fluid as incompressible if its density does not substantially change with modest changes in pressure74 . For this limiting case, ρ is constant and the continuity equation simplifies to the following form:
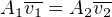
Examining this equation in light of dimensional analysis, we see that the product Av is also an expression of flow rate:
![[ ] [ ]
- m2- [m] m3-
A v = 1 s = s](https://www.technocrazed.com/books/Instrumentation/Book_half395x.png)
Cubic meters per second is an expression of volumetric flow rate, often symbolized by the variable Q:
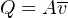
The practical implication of this principle is that fluid velocity is inversely proportional to the cross-sectional area of a pipe. That is, fluid slows down when the pipe’s diameter expands, and vice-versa. We readily see this principle manifest in the natural world: rivers run slowest where they are deep and wide, and run fastest where they are shallow and narrow.
More specifically, we may say that the average velocity of a fluid through a pipe varies inversely with the square of the diameter, since cross-sectional area is proportional to the square of the pipe diameter. For example, if fluid flows at a velocity of 2 feet per second through a 12-inch pipe, and that pipe extends to a narrower section only 6 inches (half the diameter of the wide section), the velocity at the narrower section will be four times as great (8 feet per second), since the area of that skinnier section is one-quarter the area of the wider section.
For example, consider a pipe with an inside diameter of 8 inches (2/3 of a foot), passing a liquid flow of 5 cubic feet per minute. The average velocity (v) of this fluid may be calculated as follows:
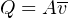
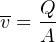
Solving for A in units of square feet:
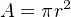
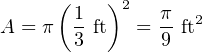
Now, solving for average velocity v:
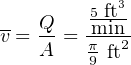
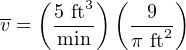
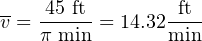
Thus, the average fluid velocity inside an 8-inch pipe passing a volumetric flow rate of 5 cubic feet per minute is 14.32 feet per minute.
2.11.12 Viscous flow
The pressure dropped by a slow-moving, viscous fluid through a pipe is described by the Hagen-Poiseuille equation. This equation applies only for conditions of low Reynolds number; i.e. when viscous forces are the dominant restraint to fluid motion through the pipe, and turbulence is nonexistent:
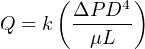
Where,
Q = Flow rate (gallons per minute)
k = Unit conversion factor = 7.86 ×105
ΔP = Pressure drop (inches of water column)
D = Pipe diameter (inches)
μ = Liquid viscosity (centipoise) – this is a temperature-dependent variable!
L = Length of pipe section (inches)
2.11.13 Bernoulli’s equation
Bernoulli’s equation is an expression of the Law of Energy Conservation for an inviscid (frictionless) fluid stream, named after Daniel Bernoulli75 . It states that the sum total energy at any point in a passive fluid stream (i.e. no pumps or other energy-imparting machines in the flow path, nor any energy-dissipating elements) must be constant. Two versions of the equation are shown here:
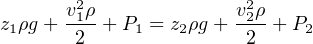
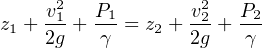
Where,
z = Height of fluid (from a common reference point, usually ground level)
ρ = Mass density of fluid
γ = Weight density of fluid (γ = ρg)
g = Acceleration of gravity
v = Velocity of fluid
P = Pressure of fluid
Each of the three terms in Bernoulli’s equation is an expression of a different kind of energy, commonly referred to as head:
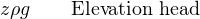
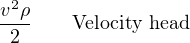

Elevation and Pressure heads are potential forms of energy, while Velocity head is a kinetic form of energy. Note how the elevation and velocity head terms so closely resemble the formulae for potential and kinetic energy of solid objects:
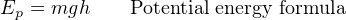
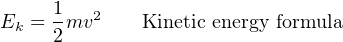
The only real differences between the solid-object and fluid formulae for energies is the use of mass density (ρ) for fluids instead of mass (m) for solids, and the arbitrary use of the variable z for height instead of h. In essence, the elevation and velocity head terms within Bernoulli’s equation come from the assumption of individual fluid molecules behaving as miniscule solid masses.
It is very important to maintain consistent units of measurement when using Bernoulli’s equation! Each of the three energy terms (elevation, velocity, and pressure) must possess the exact same units if they are to add appropriately76 . Here is an example of dimensional analysis applied to the first version of Bernoulli’s equation (using British units):
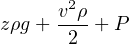
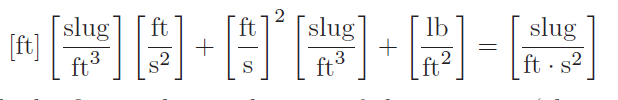
As you can see, both the first and second terms of the equation (elevation and velocity heads) bear the same unit of slugs per foot-second squared after all the “feet” are canceled. The third term (pressure head) does not appear as though its units agree with the other two terms, until you realize that the unit definition of a “pound” is a slug of mass multiplied by the acceleration of gravity in feet per second squared, following Newton’s Second Law of motion (F = ma):
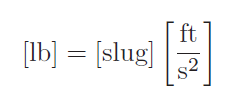
Once we make this substitution into the pressure head term, the units are revealed to be the same as the other two terms, slugs per foot-second squared:
![[ ]
[ ] ⌊slug ft ⌋ [ ]
lb- = ⌈-----s2-⌉ = slug-
ft2 ft2 ft⋅s2](https://www.technocrazed.com/books/Instrumentation/Book_half415x.png)
In order for our British units to be consistent here, we must use feet for elevation, slugs per cubic foot for mass density, feet per second squared for acceleration, feet per second for velocity, and pounds per square foot for pressure. If one wished to use the more common pressure unit of PSI (pounds per square inch) with Bernoulli’s equation instead of PSF (pounds per square foot), all the other units would have to change accordingly: elevation in inches, mass density in slugs per cubic inch, acceleration in inches per second squared, and velocity in inches per second.
Just for fun, we can try dimensional analysis on the second version of Bernoulli’s equation, this time using metric units:
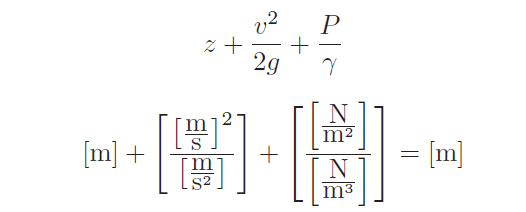
Here, we see that all three terms end up being cast in simple units of meters. That is, the fluid’s elevation, velocity, and pressure heads are all expressed as simple elevations. In order for our metric units to be consistent here, we must use meters for elevation, meters per second for velocity, meters per second squared for acceleration, pascals (newtons per square meter) for pressure, and newtons per cubic meter for weight density.
Applying Bernoulli’s equation to real-life applications can be a bit daunting, as there are so many different units of measurement to contend with, and so many calculations which must be precise in order to arrive at a correct final answer. The following example serves to illustrate how Bernoulli’s equation may be applied to the solution of pressure at a point in a water piping system, assuming no frictional losses anywhere in the system:
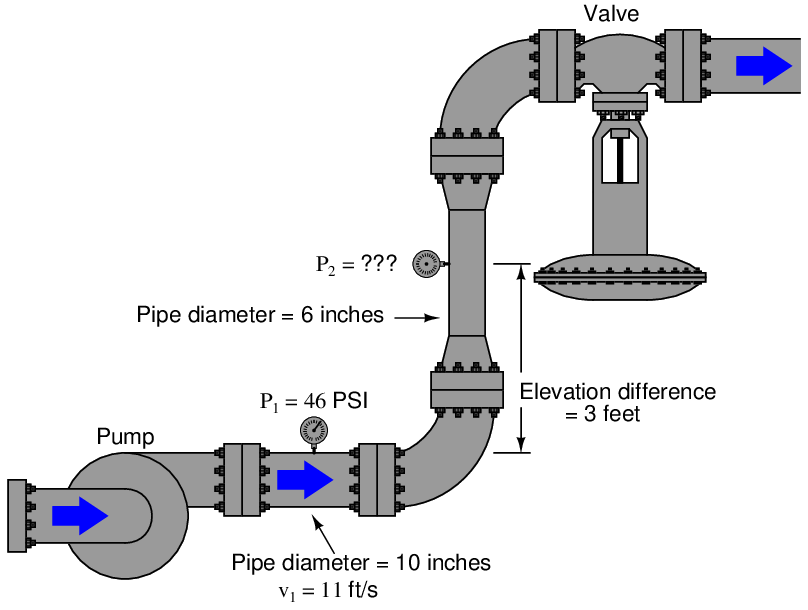
We know without a doubt that Bernoulli’s equation will be what we need to evaluate in order to solve for the unknown pressure P2, but where do we begin? A good place to start is by writing the equation we know we will need, then identifying all known values and all unknown values:
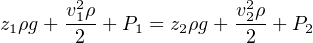
Here is a list of known values, given to us already:

The conversion for P1 from units of PSI into units of PSF is quite simple: multiply 46 PSI by 144 to get 6624 PSF.
Here is a list of values unknown to us at this time:

Now all we must do is solve for ρ and v2, and we will be ready to use Bernoulli’s equation to solve for P2. The important of identifying all the known and unknown quantities before beginning any calculations cannot be overstated. Doing so allows us to develop a plan for solving the problem. Without a plan, one has no idea of where or how to proceed, which is a condition many students repeatedly find themselves in when solving physics-type problems.
We know that ρ is an expression of mass density for the fluid, and we were told the fluid in this example is water. Water has a maximum density of 62.4 pounds per cubic foot, but this figure is not usable in our chosen form of Bernoulli’s equation because it is weight density (γ) and not mass density (ρ).
The relationship between weight density γ and mass density ρ is the exact same relationship between weight (FW) and mass (m) in a gravitational field (g). Newton’s Second Law equation relating force to mass and acceleration (F = ma) works well to relate weight to mass and gravitational acceleration:
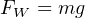
Dividing both sides of this equation by volumetric units (V ) (e.g. cubic feet) gives us our relationship between γ and ρ:
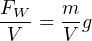
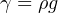
Water has a weight density of 62.4 pounds per cubic foot in Earth gravity (32.2 feet per second squared), so:
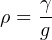
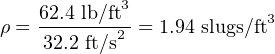
Now we may calculate the total value for the left-hand side of Bernoulli’s equation, representing the sum total of potential and kinetic heads for the fluid within the 10-inch pipe:
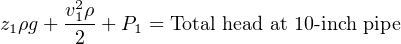

Note the absolutely consistent use of units: all units of distance are feet. All units of mass as slugs. All units of time are seconds. Failure to maintain consistency of units will result in (often severely) incorrect results!77
There is one more unknown quantity to solve for before we may calculate values at the 6-inch pipe, and that unknown quantity is v2. We know that the Continuity equation gives us a mathematical relationship between volumetric flow (Q), pipe area (A), and velocity (v):
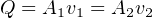
Looking at this equation, the only variable we know the value of at this point is v1, and we need to find v2. However, if we could find the values of A1 and A2, and/or Q, we would have the information we need to solve for v2, which in turn would give us the information we would need to solve for P2 in Bernoulli’s equation.
One way to approach this problem is to express the areas and velocities as ratios, eliminating Q entirely so all we need to find are A1 and A2:
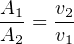
The area of a circular pipe is given by the basic equation A = πr2. Since the problem gives us each pipe’s diameter (10 inches and 6 inches), we know the radii (5 inches and 3 inches, respectively) which we may then plug into our ratio equation:
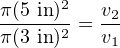
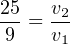
Knowing v1 has a value of 11 feet per second, the solution for v2 is now quite simple:
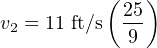
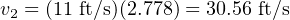
Finally, we have all the pieces necessary to solve for P2 in the right-hand side of Bernoulli’s equation:
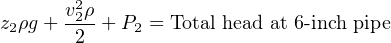

Knowing that the total head calculated at the first location was 6741.4 lb/ft2, and the Conservation of Energy requires total heads at both locations be equal (assuming no energy lost to fluid friction along the way), P2 must be equal to:
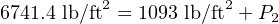
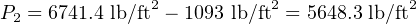
Converting pounds per square foot into the more customary unit of pounds per square inch (PSI):
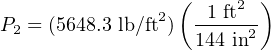
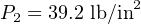
Before discussing the larger meaning of our solution, it would be good to review the problem-solving plan we followed to calculate P2:
First, we identified Bernoulli’s equation as being the central equation necessary for solving P2. Then, we identified all the known variables within Bernoulli’s equation given to us in the problem, and also if there were any unit-conversion operations necessary. Next, we identified any unknown variables necessary to solve for P2 in Bernoulli’s equation. For each of those unknown variables, we found or developed equations to solve for them, based on variables known to us. The graphic shown above illustrates our plan of solution, with arrows showing the dependent relationships where equations supplied values for unknown quantities in other equations.
This is not just a problem-solving technique unique to Bernoulli’s equation; it is a general strategy applicable to any type of problem where multiple equations must be used to solve for some quantity. The study of physics is general is filled with problems like this!
Note how our calculated value for P2 at the second gauge is so much lower than the pressure at the first gauge: 39.2 PSI compared to 46 PSI. This represents nearly a 7 PSI decrease in pressure! Note also how little vertical distance separates the two gauges: only 3 feet. Clearly, the change in elevation between those two points in insufficient to account for the large loss in pressure78 . Given a 3 foot difference in elevation, one would expect a pressure reduction of about 1.3 PSI for a static column of water, but what we’re seeing in this piping system is a pressure drop of nearly 7 PSI. The difference is due to an exchange of energy from potential to kinetic form, as the fluid enters a much narrower pipe (6 inches instead of 10) and must increase velocity.
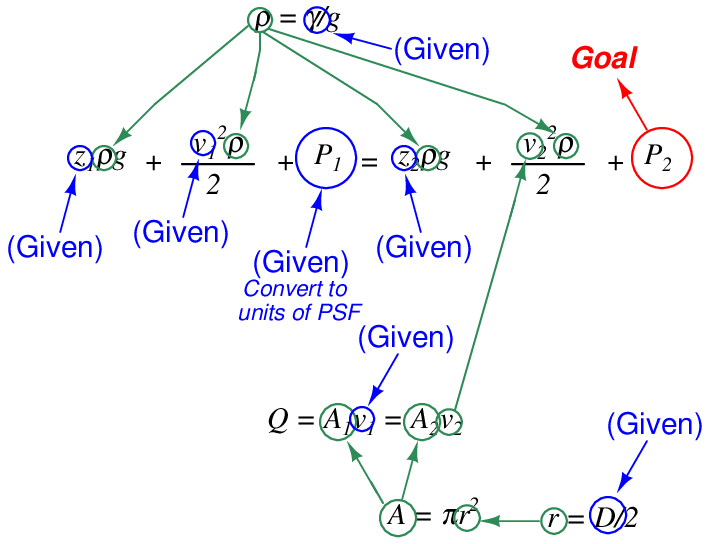
Furthermore, if we were to increase the flow rate discharged from the pump, resulting in even more velocity through the narrow pipe, pressure at P2 might even drop lower than atmospheric. In other words, Bernoulli’s equation tells us we can actually produce a vacuum by accelerating a fluid through a constriction. This principle is widely used in industry with devices known as eductors or ejectors79 : tapered tubes through which fluid flows at high velocity to produce a vacuum at the throat.
This, in fact, is how a carburetor works in an older automobile engine to vaporize liquid gasoline fuel into a stream of air drawn into the engine: the engine’s intake air passes through a venturi tube, where vacuum at the throat of the venturi produces enough negative pressure to draw liquid gasoline into the stream to produce a fine mist.
Ejectors use a high-velocity gas or vapor (e.g. superheated steam) to produce significant vacuums. Eductors use process liquid flow, such as the eductor shown in this next photograph where wastewater flow creates a vacuum to draw gaseous chlorine into the stream for biological disinfection:

Here, the eductor helps fulfill an important safety function. By creating a vacuum to draw toxic chlorine gas from the supply tank into the water stream, the chlorine gas piping may be continuously maintained at a slightly negative pressure throughout. If ever a leak were to develop in the chlorine system, this vacuum would cause ambient air to enter the chlorine pipe rather than toxic chlorine gas to exit the pipe, making a leak far less dangerous than if the chlorine gas piping were maintained in a pressurized state.
2.11.14 Torricelli’s equation
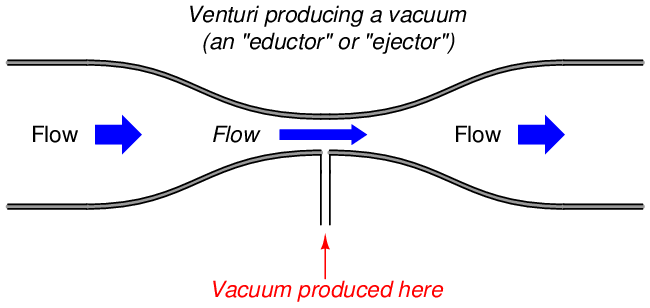
The velocity of a liquid stream exiting from a nozzle, pressured solely by a vertical column of that same liquid, is equal to the free-fall velocity of a solid mass dropped from the same height as the top of the liquid column. In both cases, potential energy (in the form of vertical height) converts to kinetic energy (motion):
This was discovered by Evangelista Torricelli almost 100 years prior to Bernoulli’s more comprehensive formulation. The velocity may be determined by solving for v after setting the potential and kinetic energy formulae equal to each other (since all potential energy at the upper height must translate into kinetic energy at the bottom, assuming no frictional losses):
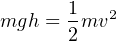
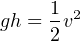
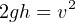
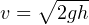
Note how mass (m) simply disappears from the equation, neatly canceling on both sides. This means the nozzle velocity depends only on height, not the mass density of the liquid. It also means the velocity of the falling object depends only on height, not the mass of the object.
2.11.15 Flow through a venturi tube
If an incompressible fluid moves through a venturi tube (i.e. a tube purposefully built to be narrow in the middle), the continuity principle tells us the fluid velocity must increase through the narrow portion. This increase in velocity causes kinetic energy to increase at that point. If the tube is level, there will be negligible difference in elevation (z) between different points of the tube’s centerline, which means elevation head remains constant. According to the Law of Energy Conservation, some other form of energy must decrease to account for the increase in kinetic energy. This other form is the pressure head, which decreases at the throat of the venturi:
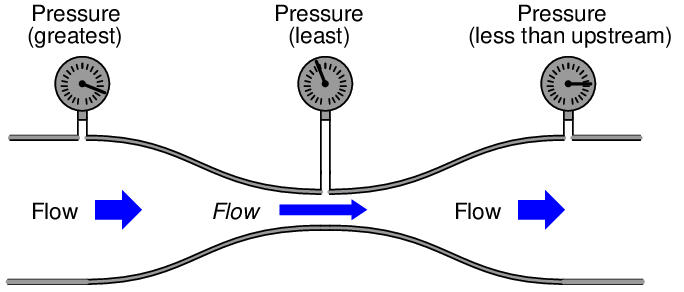
Ideally, the pressure downstream of the narrow throat should be the same as the pressure upstream, assuming equal pipe diameters upstream and down. However, in practice the downstream pressure gauge will show slightly less pressure than the upstream gauge due to some inevitable energy loss as the fluid passed through the venturi. Some of this loss is due to fluid friction against the walls of the tube, and some is due to viscous losses within the fluid driven by turbulent fluid motion at the high-velocity throat passage.
The difference between upstream and downstream pressure is called permanent pressure loss, while the difference in pressure between the narrow throat and downstream is called pressure recovery.
If we install vertical sight-tubes called piezometers80 along a horizontal venturi tube, the differences in pressure will be shown by the heights of liquid columns within the tubes. Here, we assume an ideal (inviscid) liquid with no permanent pressure loss:
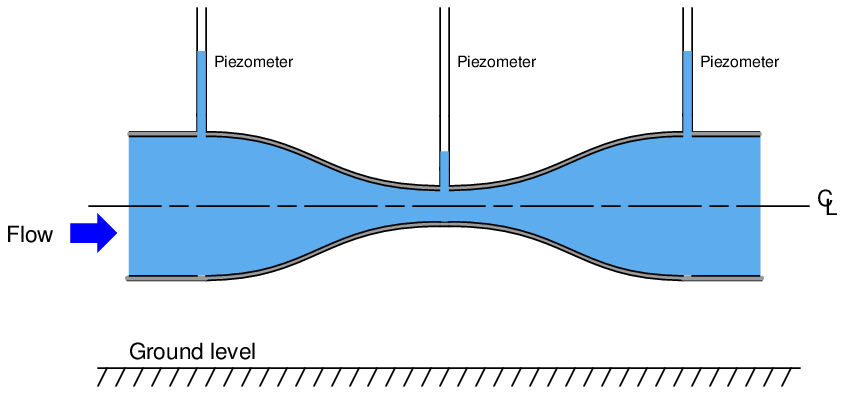
The height of liquid in each piezometer tube represents the amount of potential energy81 in the fluid at that point along the venturi tube.
We may gain more insight into the nature of energy in this moving fluid stream if we add three more piezometers, each one equipped with its own Pitot tube facing upstream to “catch” the velocity of the fluid. Rather than represent potential energy by liquid height as the straight-tube piezometers do, the Pitot tube piezometers represent the total energy (potential plus kinetic) of the fluid. As such, the liquid heights in these new piezometers are all equal to each other, showing that total energy is indeed conserved at every point in the system:
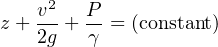
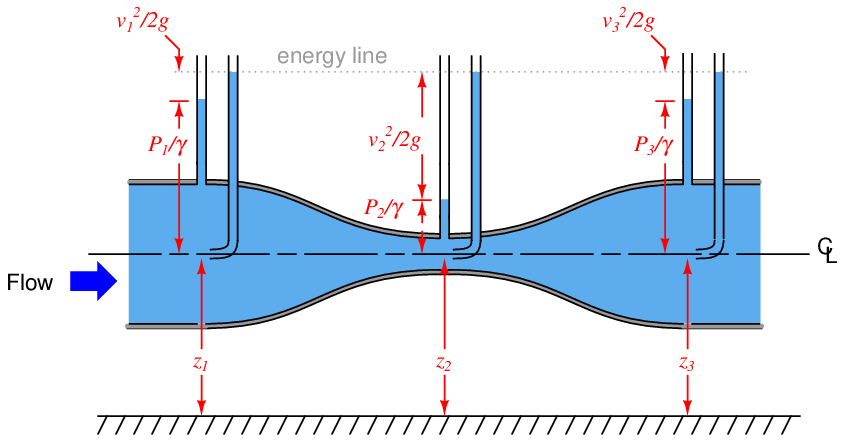
Here, each of the “heads” represented82 in Bernoulli’s equation are shown in relation to the different piezometer heights. The difference in liquid column height between each Pitot tube piezometer (potential + kinetic energy) and its corresponding straight-tube piezometer (potential energy alone) reflects the amount of kinetic energy possessed by the fluid stream at that point in the venturi tube.
In a real venturi tube, there is some energy permanently lost in the moving fluid due to friction. Consequently the piezometer measurements in a real venturi tube would look something like this:
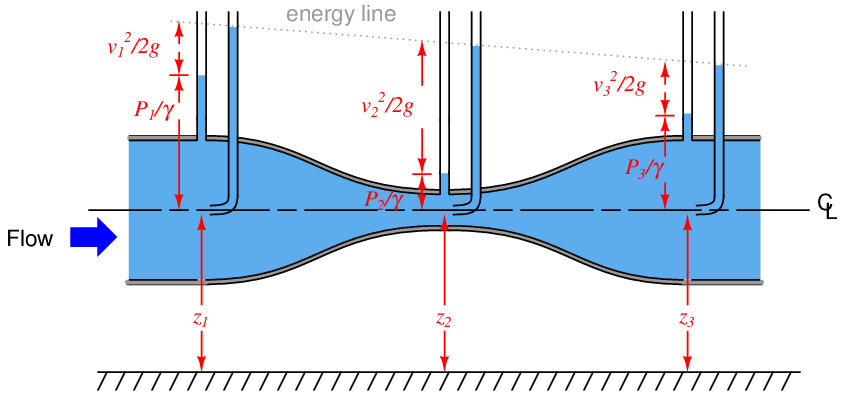
The “energy line” is seen to slope downhill from inlet to outlet on the venturi tube, showing a degradation in total energy content from beginning to end.
References
Caupin, F. and Herbert, C., Cavitation in Water: A Review, C.R. Physique 7, pages 1000-1017, 2006.
Chow, Ven Te., Open-Channel Hydraulics, McGraw-Hill Book Company, Inc., New York, NY, 1959.
Considine, Douglas C., Energy Technology Handbook, McGraw-Hill Book Company, New York, NY, 1977.
Control Valve Handbook, Third Edition, Fisher Controls International, Inc., Marshalltown, IA, 1999.
Coy, John J.; Townsend, Dennis P.; and Zaretsky, Erwin V., Gearing, NASA Reference Publication 1152, AVSCOM Technical Report 84-C-15, National Aeronautics and Space Administration, Scientific and Technical Information Branch, Cleveland, OH, 1985.
Faydor, L. Litvin; Egelja, A.; Tan, J.; Chen, D.Y-D.; and Heath, G., Handbook on Face Gear Drives With a Spur Involute Pinion, University of Illinois at Chicago report E-12127, NASA report NASA CR-2000-209909, U.S. Army Research Laboratory report ARL-CR-447, National Aeronautics and Space Administration, Washington D.C., March 2000.
Faydor, L. Litvin; Fuentes, Alfonso; Vecchiato, Daniele; and Gonzalez-Perez, Ignacio, New Design and Improvement of Planetary Gear Trains, University of Illinois at Chicago report E-14576, NASA report NASA CR-2004-213101, U.S. Army Research Laboratory report ARL-CR-0540, National Aeronautics and Space Administration, Washington D.C., July 2004.
Giancoli, Douglas C., Physics for Scientists & Engineers, Third Edition, Prentice Hall, Upper Saddle River, NJ, 2000.
Hicks, Tyler G., Standard Handbook of Engineering Calculations, McGraw-Hill, Inc., New York, NY, 1972.
Lipták, Béla G. et al., Instrument Engineers’ Handbook – Process Measurement and Analysis Volume I, Fourth Edition, CRC Press, New York, NY, 2003.
Miller, Richard W., Flow Measurement Engineering Handbook, Second Edition, McGraw-Hill Publishing Company, New York, NY, 1989.
Pauling, Linus, General Chemistry, Dover Publications, Inc., Mineola, NY, 1988.
Rouse, Hunter, Characteristics of Laminar and Turbulent Flow (video), Iowa Institute of Hydraulic Research, University of Iowa.
Shapiro, Ascher H., Pressure Fields and Fluid Acceleration (video), Massachusetts Institute of Technology, Educational Services Incorporated, 1962.
Thompson, Ambler and Taylor, Barry N., Guide for the Use of the International System of Units (SI), special publication 811 (second printing), National Institute of Standards and Technology, Gaithersburg, MD, 2008.
Vennard, John K., Elementary Fluid Mechanics, 3rd Edition, John Wiley & Sons, Inc., New York, NY, 1954.
Wall, Göran, Exergetics, Bucaramanga, January 2009.
Weast, Robert C.; Astel, Melvin J.; and Beyer, William H., CRC Handbook of Chemistry and Physics, 64th Edition, CRC Press, Inc., Boca Raton, FL, 1984.