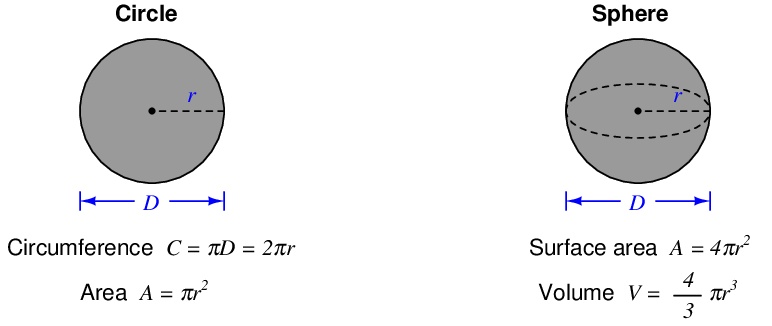Mass (m) is the opposition an object has to acceleration (changes in velocity). Weight is the force (F) imposed on a mass by a gravitational field. Mass is an intrinsic property of an object, regardless of the environment. Weight, on the other hand, depends on the strength of the gravitational field in which the object resides. A 20 kilogram slug of metal has the exact same mass whether it rests on Earth, or in the zero-gravity environment of outer space, or on the surface of the planet Jupiter. However, the weight of that mass depends on gravity: zero weight in outer space (where there is no gravity to act upon it), some weight on Earth, and a much greater amount of weight on the planet Jupiter (due to the much stronger gravitational field of that planet).
Since mass is the opposition of an object to changes in velocity (acceleration), it stands to reason force, mass, and acceleration for any particular object are directly related to one another:
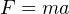
Where,
F = Force in newtons (metric) or pounds (British)
m = Mass in kilograms (metric) or slugs (British)
a = Acceleration in meters per second squared (metric) or feet per second squared (British)
If the force in question is the weight of the object, then the acceleration (a) in question is the acceleration constant of the gravitational field where the object resides. For Earth at sea level, agravity is approximately 9.81 meters per second squared, or 32.2 feet per second squared. Earth’s gravitational acceleration constant is usually represented in equations by the variable letter g instead of the more generic a.
Since acceleration is nothing more than the rate of velocity change with respect to time, the force/mass equation may be expressed using the calculus notation of the first derivative:
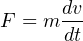
Where,
F = Force in newtons (metric) or pounds (British)
m = Mass in kilograms (metric) or slugs (British)
v = Velocity in meters per second (metric) or feet per second (British)
t = Time in seconds
Since velocity is nothing more than the rate of position change with respect to time, the force/mass equation may be expressed using the calculus notation of the second derivative (acceleration being the derivative of velocity, which in turn is the derivative of position):
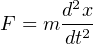
Where,
F = Force in newtons (metric) or pounds (British)
m = Mass in kilograms (metric) or slugs (British)
x = Position in meters (metric) or feet (British)
t = Time in seconds
Mass density (ρ) for any substance is the proportion of mass to volume. Weight density (γ) for any substance is the proportion of weight to volume.
Just as weight and mass are related to each other by gravitational acceleration, weight density and mass density are also related to each other by gravity:
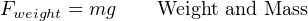
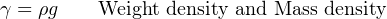
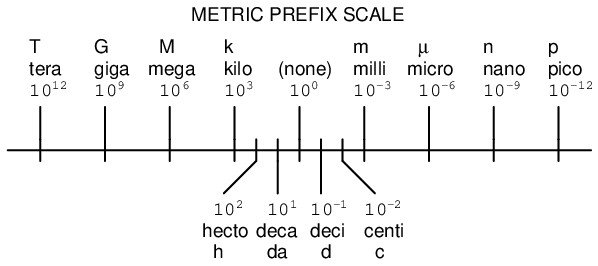
2.2 Metric prefixes
2.3 Areas and volumes
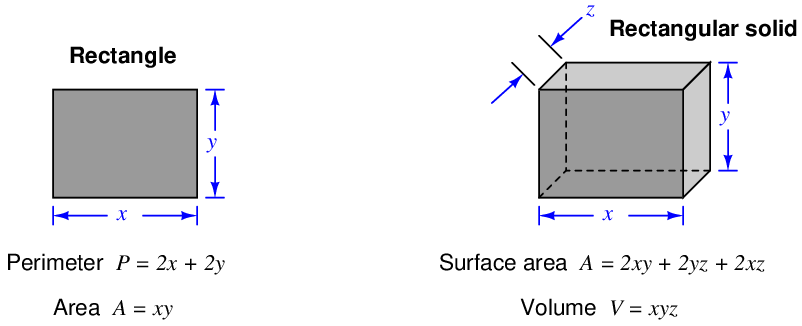
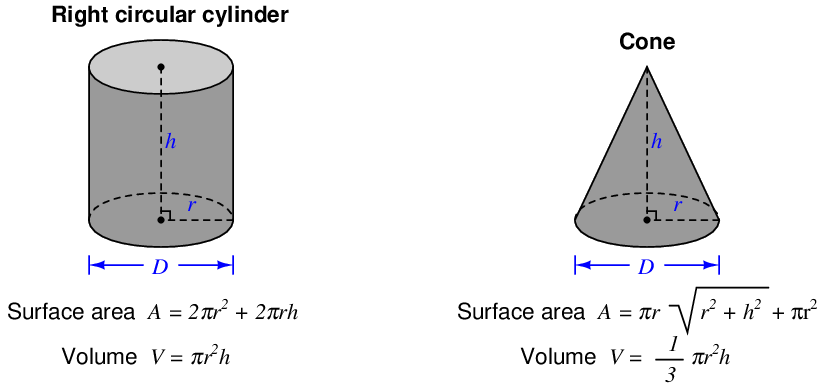
Area refers to the size of two-dimensional surface. Volume refers to the size of a three-dimensional space. To put both these measures into context; the question of how much paint will be required to adequately cover a house is one of area, while the question of how much water will be required to fill a pond is one of volume.
Some units of measurement for area and volume are nothing more than compounded linear units. Ten centimeters is an expression of distance, while ten square centimeters (cm2) is an expression of area, and ten cubic centimeters (cm3) is an expression of volume. It important to note that the modifiers “square” and “cubic” do not in any way imply the object in question is square or cubic in shape. It is perfectly reasonable to measure the area of a circle, for instance, using the unit of square centimeters.
Other units of spatial measurement are specific to area or to volume. The acre, for example, is a unit of area measurement developed for the purpose of quantifying the size of land plots, one acre being equivalent to 43560 square feet. An example of a unit specifically devoted to volume measurement is the liter, equivalent to 1000 cubic centimeters.
2.3.1 Common geometric shapes