In our study of AC circuits thus far, we’ve explored circuits powered by a single-frequency sine voltage waveform. In many applications of electronics, though, single-frequency signals are the exception rather than the rule. Quite often we may encounter circuits where multiple frequencies of voltage coexist simultaneously. Also, circuit waveforms may be something other than sine-wave shaped, in which case we call them non-sinusoidal waveforms.
Additionally, we may encounter situations where DC is mixed with AC: where a waveform is superimposed on a steady (DC) signal. The result of such a mix is a signal varying in intensity, but never changing polarity, or changing polarity asymmetrically (spending more time positive than negative, for example). Since DC does not alternate as AC does, its “frequency” is said to be zero, and any signal containing DC along with a signal of varying intensity (AC) may be rightly called a mixed-frequency signal as well. In any of these cases where there is a mix of frequencies in the same circuit, analysis is more complex than what we’ve seen up to this point.
Coupling
Sometimes mixed-frequency voltage and current signals are created accidentally. This may be the result of unintended connections between circuits—called coupling—made possible by stray capacitance and/or inductance between the conductors of those circuits. A classic example of coupling phenomenon is seen frequently in industry where DC signal wiring is placed in close proximity to AC power wiring. The nearby presence of high AC voltages and currents may cause “foreign” voltages to be impressed upon the length of the signal wiring. Stray capacitance formed by the electrical insulation separating power conductors from signal conductors may cause voltage (with respect to earth ground) from the power conductors to be impressed upon the signal conductors, while stray inductance formed by parallel runs of wire in conduit may cause current from the power conductors to electromagnetically induce voltage along the signal conductors. The result is a mix of DC and AC at the signal load. The following schematic shows how an AC “noise” source may “couple” to a DC circuit through mutual inductance (Mstray) and capacitance (Cstray) along the length of the conductors. (Figure below)
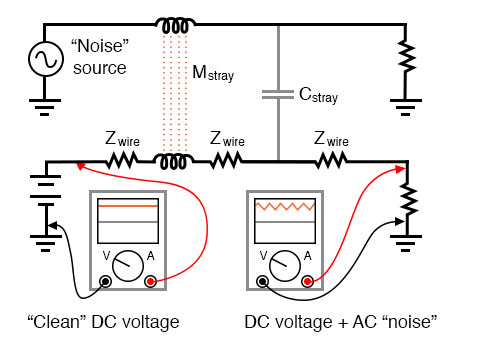
Stray inductance and capacitance couple stray AC into desired DC signal.
When stray AC voltages from a “noise” source mix with DC signals conducted along signal wiring, the results are usually undesirable. For this reason, power wiring and low-level signal wiring should always be routed through separated, dedicated metal conduit, and signals should be conducted via 2-conductor “twisted pair” cable rather than through a single wire and ground connection: (Figure below)
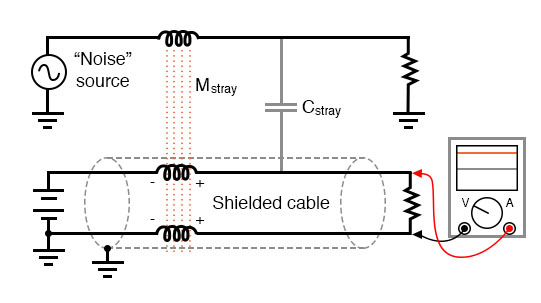
Shielded twisted pair minimized noise.
The grounded cable shield—a wire braid or metal foil wrapped around the two insulated conductors—isolates both conductors from electrostatic (capacitive) coupling by blocking any external electric fields, while the parallel proximity of the two conductors effectively cancels any electromagnetic (mutually inductive) coupling because any induced noise voltage will be approximately equal in magnitude and opposite in phase along both conductors, canceling each other at the receiving end for a net (differential) noise voltage of almost zero. Polarity marks placed near each inductive portion of signal conductor length shows how the induced voltages are phased in such a way as to cancel one another.
Coupling may also occur between two sets of conductors carrying AC signals, in which case both signals may become “mixed” with each other:

Coupling of AC signals between parallel conductors.
Coupling is but one example of how signals of different frequencies may become mixed. Whether it be AC mixed with DC, or two AC signals mixing with each other, signal coupling via stray inductance and capacitance is usually accidental and undesired. In other cases, mixed-frequency signals are the result of intentional design or they may be an intrinsic quality of a signal. It is generally quite easy to create mixed-frequency signal sources. Perhaps the easiest way is to simply connect voltage sources in series: (Figure below)
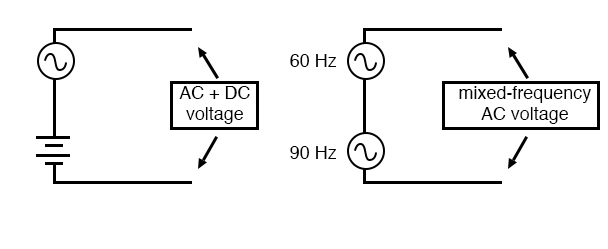
Series connection of voltage sources mixes signals.
Some computer communications networks operate on the principle of superimposing high-frequency voltage signals along 60 Hz power-line conductors, so as to convey computer data along existing lengths of power cabling. This technique has been used for years in electric power distribution networks to communicate load data along high-voltage power lines. Certainly these are examples of mixed-frequency AC voltages, under conditions that are deliberately established.
In some cases, mixed-frequency signals may be produced by a single voltage source. Such is the case with microphones, which convert audio-frequency air pressure waves into corresponding voltage waveforms. The particular mix of frequencies in the voltage signal output by the microphone is dependent on the sound being reproduced. If the sound waves consist of a single, pure note or tone, the voltage waveform will likewise be a sine wave at a single frequency. If the sound wave is a chord or other harmony of several notes, the resulting voltage waveform produced by the microphone will consist of those frequencies mixed together. Very few natural sounds consist of single, pure sine wave vibrations but rather are a mix of different frequency vibrations at different amplitudes.
Fundamental and Harmonic Frequencies
Musical chords are produced by blending one frequency with other frequencies of particular fractional multiples of the first. However, investigating a little further, we find that even a single piano note (produced by a plucked string) consists of one predominant frequency mixed with several other frequencies, each frequency a whole-number multiple of the first (called harmonics, while the first frequency is called the fundamental). An illustration of these terms is shown in Table below with a fundamental frequency of 1000 Hz (an arbitrary figure chosen for this example).
For a “base” frequency of 1000 Hz:
| Frequency | Term |
|---|---|
| 1000 | 1st harmonic, or fundamental |
| 2000 | 2nd harmonic |
| 3000 | 3rd harmonic |
| 4000 | 4th harmonic |
| 5000 | 5th harmonic |
| 6000 | 6th harmonic |
| 7000 | 7th harmonic |
Overtone
Sometimes the term “overtone” is used to describe the a harmonic frequency produced by a musical instrument. The “first” overtone is the first harmonic frequency greater than the fundamental. If we had an instrument producing the entire range of harmonic frequencies shown in the table above, the first overtone would be 2000 Hz (the 2nd harmonic), while the second overtone would be 3000 Hz (the 3rd harmonic), etc. However, this application of the term “overtone” is specific to particular instruments.
It so happens that certain instruments are incapable of producing certain types of harmonic frequencies. For example, an instrument made from a tube that is open on one end and closed on the other (such as a bottle, which produces sound when air is blown across the opening) is incapable of producing even-numbered harmonics. Such an instrument set up to produce a fundamental frequency of 1000 Hz would also produce frequencies of 3000 Hz, 5000 Hz, 7000 Hz, etc, but would not produce 2000 Hz, 4000 Hz, 6000 Hz, or any other even-multiple frequencies of the fundamental. As such, we would say that the first overtone (the first frequency greater than the fundamental) in such an instrument would be 3000 Hz (the 3rd harmonic), while the second overtone would be 5000 Hz (the 5th harmonic), and so on.
A pure sine wave (single frequency), being entirely devoid of any harmonics, sounds very “flat” and “featureless” to the human ear. Most musical instruments are incapable of producing sounds this simple. What gives each instrument its distinctive tone is the same phenomenon that gives each person a distinctive voice: the unique blending of harmonic waveforms with each fundamental note, described by the physics of motion for each unique object producing the sound.
Brass instruments do not possess the same “harmonic content” as woodwind instruments, and neither produce the same harmonic content as stringed instruments. A distinctive blend of frequencies is what gives a musical instrument its characteristic tone. As anyone who has played guitar can tell you, steel strings have a different sound than nylon strings. Also, the tone produced by a guitar string changes depending on where along its length it is plucked. These differences in tone, as well, are a result of different harmonic content produced by differences in the mechanical vibrations of an instrument’s parts. All these instruments produce harmonic frequencies (whole-number multiples of the fundamental frequency) when a single note is played, but the relative amplitudes of those harmonic frequencies are different for different instruments. In musical terms, the measure of a tone’s harmonic content is called timbre or color.
Musical tones become even more complex when the resonating element of an instrument is a two-dimensional surface rather than a one-dimensional string. Instruments based on the vibration of a string (guitar, piano, banjo, lute, dulcimer, etc.) or of a column of air in a tube (trumpet, flute, clarinet, tuba, pipe organ, etc.) tend to produce sounds composed of a single frequency (the “fundamental”) and a mix of harmonics. Instruments based on the vibration of a flat plate (steel drums, and some types of bells), however, produce a much broader range of frequencies, not limited to whole-number multiples of the fundamental. The result is a distinctive tone that some people find acoustically offensive.
As you can see, music provides a rich field of study for mixed frequencies and their effects. Later sections of this chapter will refer to musical instruments as sources of waveforms for analysis in more detail.
REVIEW:
- A sinusoidal waveform is one shaped exactly like a sine wave.
- A non-sinusoidal waveform can be anything from a distorted sine-wave shape to something completely different like a square wave.
- Mixed-frequency waveforms can be accidentally created, purposely created, or simply exist out of necessity. Most musical tones, for instance, are not composed of a single frequency sine-wave, but are rich blends of different frequencies.
- When multiple sine waveforms are mixed together (as is often the case in music), the lowest frequency sine-wave is called the fundamental, and the other sine-waves whose frequencies are whole-number multiples of the fundamental wave are called harmonics.
- An overtone is a harmonic produced by a particular device. The “first” overtone is the first frequency greater than the fundamental, while the “second” overtone is the next greater frequency produced. Successive overtones may or may not correspond to incremental harmonics, depending on the device producing the mixed frequencies. Some devices and systems do not permit the establishment of certain harmonics, and so their overtones would only include some (not all) harmonic frequencies.
