Chapter 10 – DC Network Analysis
The Mesh-Current Method, also known as the Loop Current Method, is quite similar to the Branch Current method in that it uses simultaneous equations, Kirchhoff’s Voltage Law, and Ohm’s Law to determine unknown currents in a network. It differs from the Branch Current method in that it does not use Kirchhoff’s Current Law, and it is usually able to solve a circuit with less unknown variables and less simultaneous equations, which is especially nice if you’re forced to solve without a calculator.
Mesh Current, conventional method
Let’s see how this method works on the same example problem:
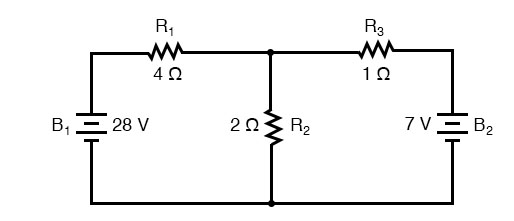
Identify Loops
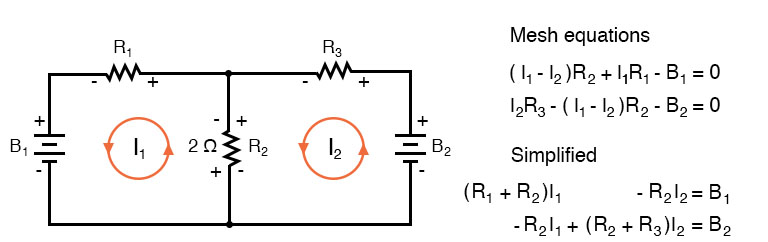
The first step in the Mesh Current method is to identify “loops” within the circuit encompassing all components. In our example circuit, the loop formed by B1, R1, and R2 will be the first while the loop formed by B2, R2, and R3 will be the second. The strangest part of the Mesh Current method is envisioning circulating currents in each of the loops. In fact, this method gets its name from the idea of these currents meshing together between loops like sets of spinning gears:
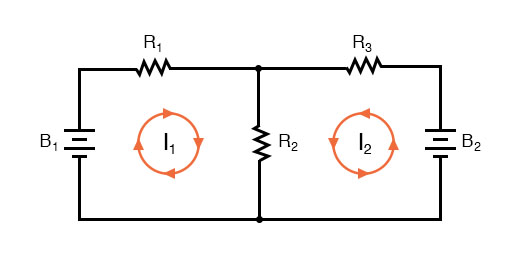
The choice of each current’s direction is entirely arbitrary, just as in the Branch Current method, but the resulting equations are easier to solve if the currents are going the same direction through intersecting components (note how currents I1 and I2 are both going “up” through resistor R2, where they “mesh,” or intersect). If the assumed direction of a mesh current is wrong, the answer for that current will have a negative value.
Label the Voltage Drop Polarities
The next step is to label all voltage drop polarities across resistors according to the assumed directions of the mesh currents. Remember that the “upstream” end of a resistor will always be negative, and the “downstream” end of a resistor positive with respect to each other, since electrons are negatively charged. The battery polarities, of course, are dictated by their symbol orientations in the diagram, and may or may not “agree” with the resistor polarities (assumed current directions):
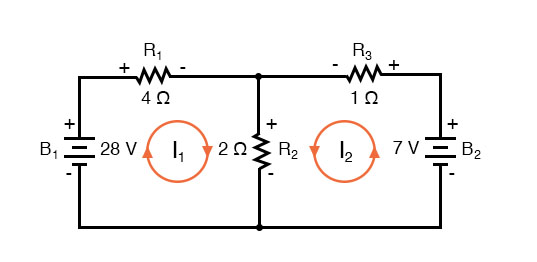
Using Kirchhoff’s Voltage Law, we can now step around each of these loops, generating equations representative of the component voltage drops and polarities. As with the Branch Current method, we will denote a resistor’s voltage drop as the product of the resistance (in ohms) and its respective mesh current (that quantity being unknown at this point). Where two currents mesh together, we will write that term in the equation with resistor current being the sum of the two meshing currents.
Tracing the Left Loop of the Circuit with Equations
Tracing the left loop of the circuit, starting from the upper-left corner and moving counter-clockwise (the choice of starting points and directions is ultimately irrelevant), counting polarity as if we had a voltmeter in hand, red lead on the point ahead and black lead on the point behind, we get this equation:
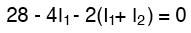
Notice that the middle term of the equation uses the sum of mesh currents I1 and I2 as the current through resistor R2. This is because mesh currents I1 and I2 are going the same direction through R2, and thus complement each other. Distributing the coefficient of 2 to the I1 and I2 terms, and then combining I1 terms in the equation, we can simplify as such:

At this time we have one equation with two unknowns. To be able to solve for two unknown mesh currents, we must have two equations. If we trace the other loop of the circuit, we can obtain another KVL equation and have enough data to solve for the two currents. Creature of habit that I am, I’ll start at the upper-left-hand corner of the right loop and trace counter-clockwise:
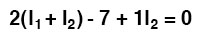
Simplifying the equation as before, we end up with:
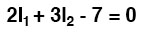
Solving For The Unknown
Now, with two equations, we can use one of several methods to mathematically solve for the unknown currents I1 and I2:

Redraw Circuit
Knowing that these solutions are values for mesh currents, not branch currents, we must go back to our diagram to see how they fit together to give currents through all components:
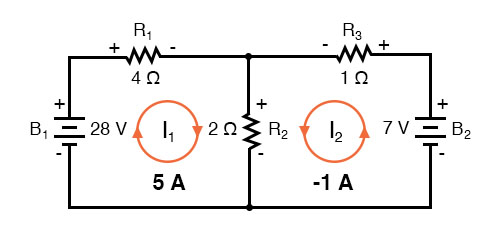
The solution of -1 amp for I2 means that we initially assumed the direction of current was incorrect. In actuality, I2 is flowing in a counter-clockwise direction at a value of (positive) 1 amp:
This change of current direction from what was first assumed will alter the polarity of the voltage drops across R2 and R3 due to current I2. From here, we can say that the current through R1 is 5 amps, with the voltage drop across R1 being the product of current and resistance (E=IR), 20 volts (positive on the left and negative on the right).
Also, we can safely say that the current through R3 is 1 amp, with a voltage drop of 1 volt (E=IR), positive on the left and negative on the right. But what is happening at R2?
Mesh current I1 is going “down” through R2, while mesh current I2 is going “up” through R2. To determine the actual current through R2, we must see how mesh currents I1 and I2 interact (in this case they’re in opposition), and algebraically add them to arrive at a final value. Since I1 is going “down” at 5 amps, and I2 is going “up” at 1 amp, the real current through R2 must be a value of 4 amps, going “down”:

A current of 4 amps through R2‘s resistance of 2 Ω gives us a voltage drop of 8 volts (E=IR), positive on the top and negative on the bottom.
Advantage of Mesh Current Analysis
The primary advantage of Mesh Current analysis is that it generally allows for the solution of a large network with fewer unknown values and fewer simultaneous equations. Our example problem took three equations to solve the Branch Current method and only two equations using the Mesh Current method. This advantage is much greater as networks increase in complexity:
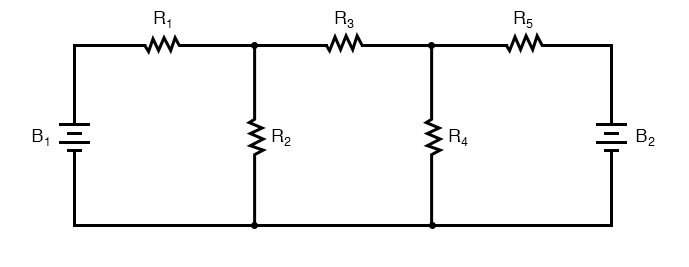
To solve this network using Branch Currents, we’d have to establish five variables to account for each and every unique current in the circuit (I1 through I5). This would require five equations for the solution, in the form of two KCL equations and three KVL equations (two equations for KCL at the nodes, and three equations for KVL in each loop):
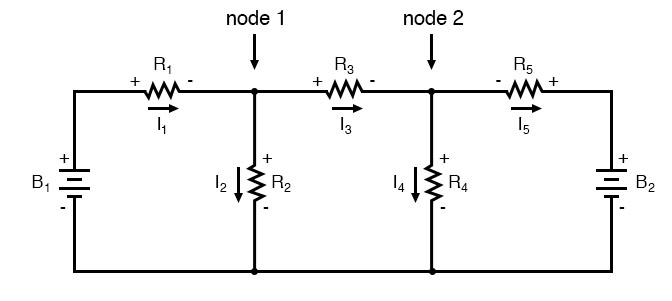

I suppose if you have nothing better to do with your time than to solve for five unknown variables with five equations, you might not mind using the Branch Current method of analysis for this circuit. For those of us who have better things to do with our time, the Mesh Current method is a whole lot easier, requiring only three unknowns and three equations to solve:
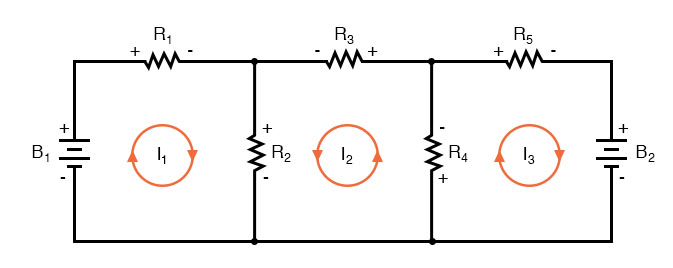
Less equations to work with is a decided advantage, especially when performing a simultaneous equation solution by hand (without a calculator).
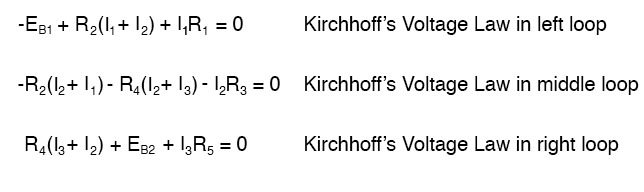
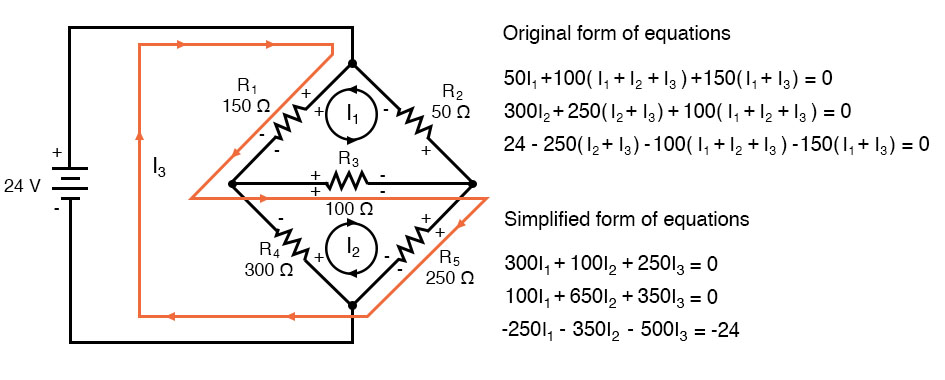
Unbalanced Wheatstone Bridge
Another type of circuit that lends itself well to Mesh Current is the unbalanced Wheatstone Bridge. Take this circuit, for example:
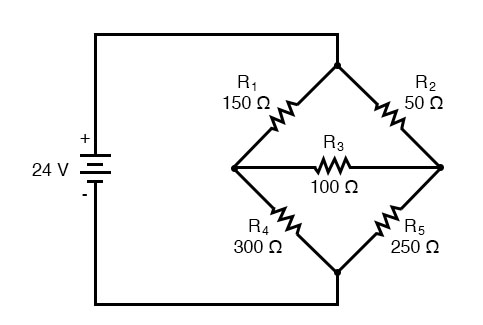
Since the ratios of R1/R4 and R2/R5 are unequal, we know that there will be the voltage across resistor R3, and some amount of current through it. As discussed at the beginning of this chapter, this type of circuit is irreducible by normal series-parallel analysis, and may only be analyzed by some other method.
We could apply the Branch Current method to this circuit, but it would require six currents (I1 through I6), leading to a very large set of simultaneous equations to solve. Using the Mesh Current method, though, we may solve for all currents and voltages with much fewer variables.
Draw Mesh
The first step in the Mesh Current method is to draw just enough mesh currents to account for all components in the circuit. Looking at our bridge circuit, it should be obvious where to place two of these currents:
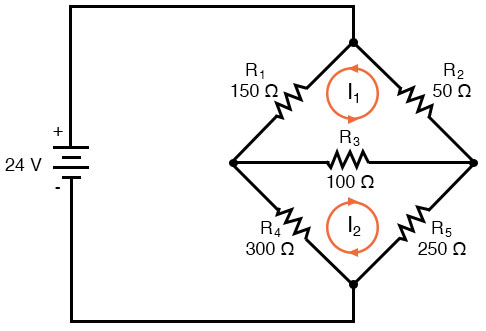
The directions of these mesh currents, of course, is arbitrary. However, two mesh currents are not enough in this circuit, because neither I1 nor I2 goes through the battery. So, we must add a third mesh current, I3:
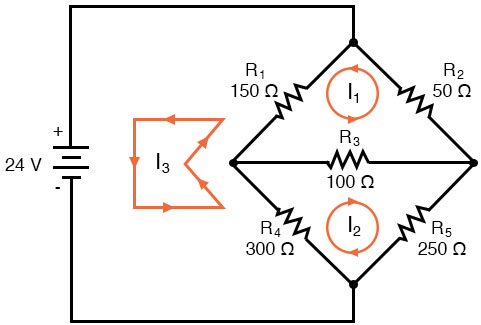
Here, I have chosen I3 to loop from the bottom side of the battery, through R4, through R1, and back to the top side of the battery. This is not the only path I could have chosen for I3, but it seems the simplest.
Label The Resistor Voltage Drop Polarities
Now, we must label the resistor voltage drop polarities, following each of the assumed currents’ directions:
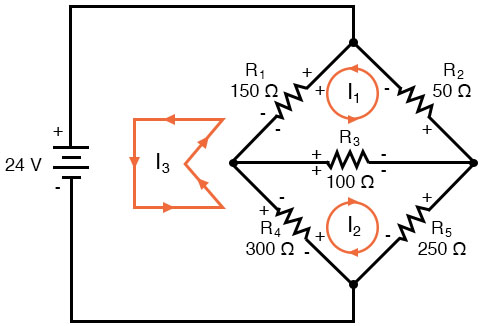
Notice something very important here: at resistor R4, the polarities for the respective mesh currents do not agree. This is because those mesh currents (I2 and I3) are going through R4 in different directions. This does not preclude the use of the Mesh Current method of analysis, but it does complicate it a bit. Though later, we will show how to avoid the R4 current clash. (See Example below)
Using KVL
Generating a KVL equation for the top loop of the bridge, starting from the top node and tracing in a clockwise direction:

In this equation, we represent the common directions of currents by their sums through common resistors. For example, resistor R3, with a value of 100 Ω, has its voltage drop represented in the above KVL equation by the expression 100(I1 + I2), since both currents I1 and I2 go through R3 from right to left. The same may be said for resistor R1, with its voltage drop expression shown as 150(I1 + I3), since both I1 and I3 go from bottom to top through that resistor, and thus work together to generate its voltage drop.
Generating a KVL equation for the bottom loop of the bridge will not be so easy since we have two currents going against each other through resistor R4. Here is how I do it (starting at the right-hand node, and tracing counter-clockwise):

Note how the second term in the equation’s original form has resistor R4‘s value of 300 Ω multiplied by the difference between I2 and I3 (I2 – I3). This is how we represent the combined effect of two mesh currents going in opposite directions through the same component. Choosing the appropriate mathematical signs is very important here: 300(I2 – I3) does not mean the same thing as 300(I3 – I2). I chose to write 300(I2 – I3) because I was thinking first of I2‘s effect (creating a positive voltage drop, measuring with an imaginary voltmeter across R4, red lead on the bottom and black lead on the top), and secondarily of I3‘s effect (creating a negative voltage drop, red lead on the bottom and black lead on the top). If I had thought in terms of I3‘s effect first and I2‘s effect secondarily, holding my imaginary voltmeter leads in the same positions (red on the bottom and black on top), the expression would have been -300(I3 – I2). Note that this expression is mathematically equivalent to the first one: +300(I2 – I3).
Well, that takes care of two equations, but I still need a third equation to complete my simultaneous equation set of three variables, three equations. This third equation must also include the battery’s voltage, which up to this point does not appear in either two of the previous KVL equations. To generate this equation, I will trace a loop again with my imaginary voltmeter starting from the battery’s bottom (negative) terminal, stepping clockwise (again, the direction in which I step is arbitrary, and does not need to be the same as the direction of the mesh current in that loop):

Solving for the Currents
Solving for I1, I2, and I3 using whatever simultaneous equation method we prefer:

Example: Use Octave to find the solution for I1, I2, and I3 from the above-simplified form of equations.
Solution: In Octave, an open-source Matlab® clone, enter the coefficients into the A matrix between square brackets with column elements comma-separated, and rows semicolon-separated. Enter the voltages into the column vector: b. The unknown currents: I1, 2, and I3 are calculated by the command: x=A\b. These are contained within the x column vector.
octave:1>A = [300,100,150;100,650,-300;-150,300,-450]
A =
300 100 150
100 650 -300
-150 300 -450
octave:2> b = [0;0;-24]
b =
0
0
-24
octave:3> x = A\b
x =
-0.093793
0.077241
0.136092
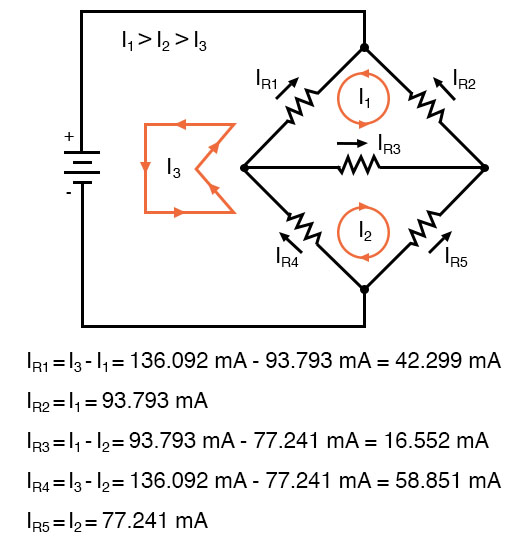
The negative value arrived at for I1 tells us that the assumed direction for that mesh current was incorrect. Thus, the actual current values through each resistor are as such:
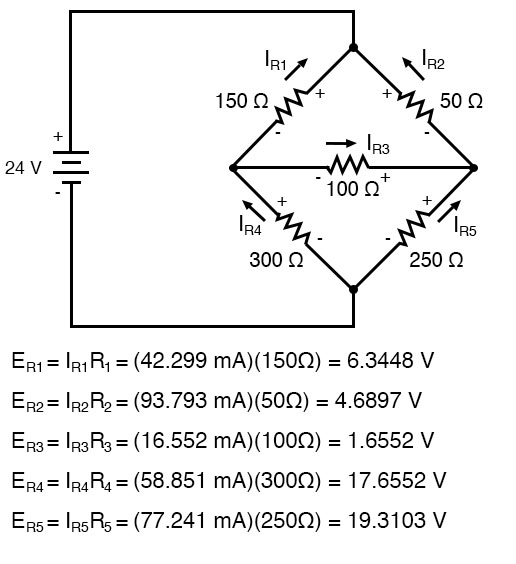
Calculating voltage drops across each resistor:
A SPICE simulation confirms the accuracy of our voltage calculations:
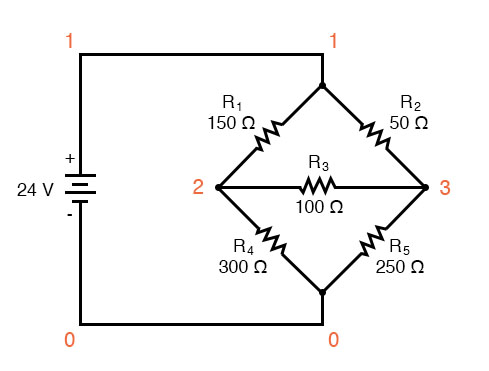
unbalanced wheatstone bridge v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .end v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01
Example:
(a) Find a new path for current I3 that does not produce a conflicting polarity on any resistor compared to I1 or I2. R4 was the offending component. (b) Find values for I1, I2, and I3. (c) Find the five resistor currents and compare them to the previous values.
Solution:
(a) Route I3 through R5, R3, and R1 as shown:
Note that the conflicting polarity on R4 has been removed. Moreover, none of the other resistors have conflicting polarities.
(b) Octave, an open source (free) Matlab clone, yields a mesh current vector at “x”:
octave:1> A = [300,100,250;100,650,350;-250,-350,-500]
A =
300 100 250
100 650 350
-250 -350 -500
octave:2> b = [0;0;-24]
b =
0
0
-24
octave:3> x = A\b
x =
-0.093793
-0.058851
0.136092
Not all currents I1, I2, and I3 are the same (I2) as the previous bridge because of different loop paths However, the resistor currents compare to the previous values:
IR1 = I1 + I3 = -93.793 ma + 136.092 ma = 42.299 ma
IR2 = I1 = -93.793 ma
IR3 = I1 + I2 + I3 = -93.793 ma -58.851 ma + 136.092 ma = -16.552 ma
IR4 = I2 = -58.851 ma
IR5 = I2 + I3 = -58.851 ma + 136.092 ma = 77.241 ma
Since the resistor currents are the same as the previous values, the resistor voltages will be identical and need not be calculated again.
REVIEW:
- Steps to follow for the “Mesh Current” method of analysis:
- (1) Draw mesh currents in loops of the circuit, enough to account for all components.
- (2) Label resistor voltage drop polarities based on assumed directions of mesh currents.
- (3) Write KVL equations for each loop of the circuit, substituting the product IR for E in each resistor term of the equation. Where two mesh currents intersect through a component, express the current as of the algebraic sum of those two mesh currents (i.e. I1 + I2) if the currents go in the same direction through that component. If not, express the current as of the difference (i.e. I1 – I2).
- (4) Solve for unknown mesh currents (simultaneous equations).
- (5) If any solution is negative, then the assumed current direction is wrong!
- (6) Algebraically add mesh currents to find current components sharing multiple mesh currents.
- (7) Solve for voltage drops across all resistors (E=IR).
Mesh current by inspection
We take a second look at the “mesh current method” with all the currents running clockwise (cw). The motivation is to simplify the writing of mesh equations by ignoring the resistor voltage drop polarity. Though, we must pay attention to the polarity of voltage sources with respect to the assumed current direction. The sign of the resistor voltage drops will follow a fixed pattern.
If we write a set of conventional mesh-current equations for the circuit below, where we do pay attention to the signs of the voltage drop across the resistors, we may rearrange the coefficients into a fixed pattern:
Once rearranged, we may write equations by inspection. The signs of the coefficients follow a fixed pattern in the pair above or the set of three in the rules below.
Mesh current rules:
- This method assumes conventional current flow voltage sources. Replace any current source in parallel with a resistor with an equivalent voltage source in series with an equivalent resistance.
- Ignoring current direction or voltage polarity on resistors, draw counterclockwise current loops traversing all components. Avoid nested loops.
- Write voltage-law equations in terms of unknown currents: I1, I2, and I3. Equation 1 coefficient 1, equation 2, coefficient 2, and equation 3 coefficient 3 are the positive sums of resistors around the respective loops.
- All other coefficients are negative, representative of the resistance common to a pair of loops. Equation 1 coefficient 2 is the resistor common to loops 1 and 2, coefficient 3 the resistor common to loops 1 an 3. Repeat for other equations and coefficients.
- +(sum of R’s loop 1)I1 – (common R loop 1-2)I2 – (common R loop 1-3)I3 = E1
-(common R loop 1-2)I1 + (sum of R’s loop 2)I2 – (common R loop 2-3)I3 = E2
-(common R loop 1-3)I1 – (common R loop 2-3)I2 + (sum of R’s loop 3)I3 = E3 - The right-hand side of the equations is equal to an electron current flow voltage source. A voltage rise with respect to the counterclockwise assumed current is positive, and 0 for no voltage source.
- Solve equations for mesh currents: I1, I2, and I3. Solve for currents through individual resistors with KCL. Solve for voltages with Ohms Law and KVL.
While the above rules are specific for a three mesh circuit, the rules may be extended to smaller or larger meshes. The figure below illustrates the application of the rules. The three currents are all drawn in the same direction, clockwise. One KVL equation is written for each of the three loops. Note that there is no polarity drawn on the resistors. We do not need it to determine the signs of the coefficients. Though we do need to pay attention to the polarity of the voltage source with respect to the current direction. The I3clockwise current flows out from the (+) positive terminal of the l24V source then returns to the (-) terminal. This is a voltage rise for conventional current flow. Therefore, the third equation right-hand side is -24V.
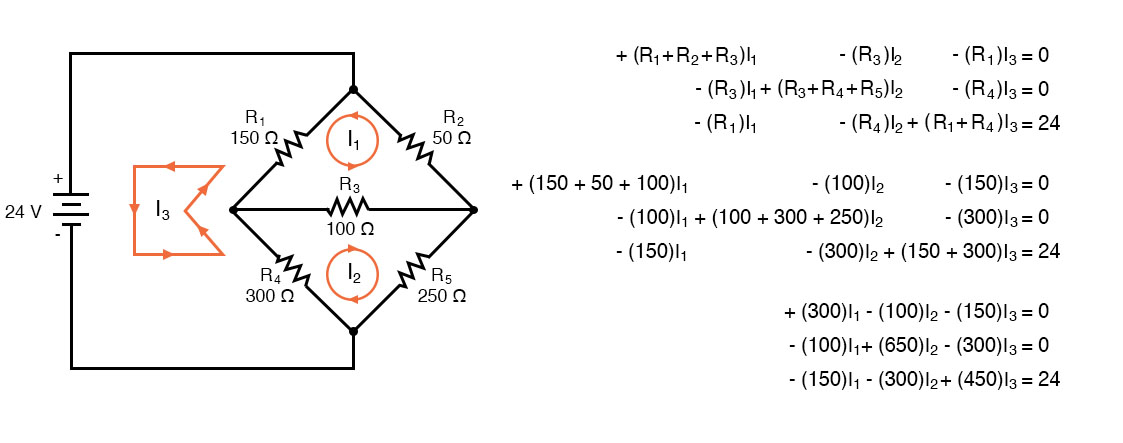
In Octave, enter the coefficients into the A matrix with column elements comma-separated, and rows semicolon-separated. Enter the voltages into the column vector b. Solve for the unknown currents: I1, I2, and I3 with the command: x=A\b. These currents are contained within the x column vector. The positive values indicate that the three mesh currents all flow in the assumed clockwise direction.
octave:2> A=[300,-100,-150;-100,650,-300;-150,-300,450]
A =
300 -100 -150
-100 650 -300
-150 -300 450
octave:3> b=[0;0;24]
b =
0
0
24
octave:4> x=A\b
x =
0.093793
0.077241
0.136092
The mesh currents match the previous solution by a different mesh current method. The calculation of resistor voltages and currents will be identical to the previous solution. No need to repeat here.
Note that electrical engineering texts are based on conventional current flow. The loop-current, mesh-current method in those texts will run the assumed mesh currents clockwise. The conventional current flows out the (+) terminal of the battery through the circuit, returning to the (-) terminal. A conventional current-voltage rise corresponds to tracing the assumed current from (-) to (+) through any voltage sources.
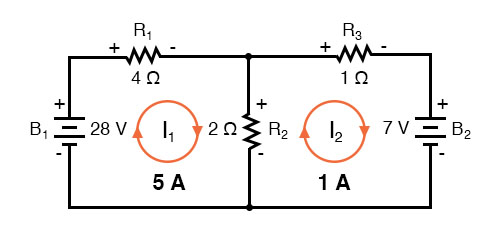
One more example of a previous circuit follows. The resistance around loop 1 is 6 Ω, around loop 2: 3 Ω. The resistance common to both loops is 2 Ω. Note the coefficients of I1 and I2 in the pair of equations. Tracing the assumed clockwise loop 1 current through B1 from (+) to (-) corresponds to an electron current flow voltage rise.
Thus, the sign of the 28 V is positive. The loop 2 counterclockwise assumed current traces (-) to (+) through B2, a voltage drop. Thus, the sign of B2 is negative, -7 in the 2nd mesh equation. Once again, there are no polarity markings on the resistors. Nor do they figure into the equations.
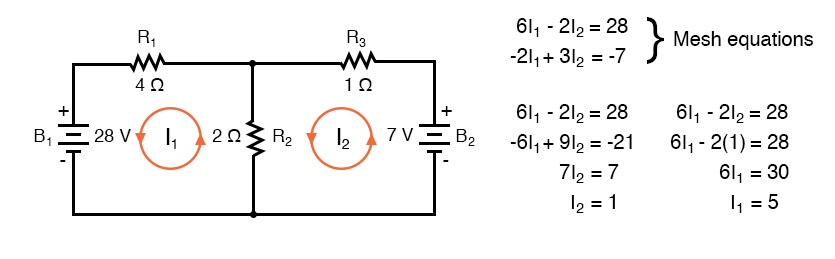
The currents I1 = 5 A, and I2 = 1 A are both positive. They both flow in the direction of the clockwise loops. This compares with previous results.
Summary:
- The modified mesh-current method avoids having to determine the signs of the equation coefficients by drawing all mesh currents clockwise for conventional current flow.
- However, we do need to determine the sign of any voltage sources in the loop. The voltage source is positive if the assumed ccw current flows with the battery (source). The sign is negative if the assumed ccw current flows against the battery.
- See the rules above for details.